Дипломная работа: Высшая математика для менеджеров
Если векторы a и b коллинеарны, то sin(a^b ) = 0 и [ab ] = 0, в частности, [aa ] = 0. Векторные произведения ортов: [ij ] = k, [jk ] = i , [ki ] = j .
Если векторы a и b заданы в базисе i, j, k координатами a (a1 , a2 , a3 ), b (b1 , b2 , b3 ), то
[ab ] =  =`i (a2 b3 - a3 b2 ) - `j (a1 b3 - a3 b1 ) + `k (a1 b2 - a2 b1 ).
=`i (a2 b3 - a3 b2 ) - `j (a1 b3 - a3 b1 ) + `k (a1 b2 - a2 b1 ).
Если векторное произведение двух векторов а и b скалярно умножается на третий вектор c, то такое произведение трех векторов называется смешанным произведением и обозначается символом a b c.
Если векторы a, b и c в базисе i, j, k заданы своими координатами a (a1 , a2 , a3 ), b (b1 , b2 , b3 ), c (c1 , c2 , c3 ), то
abc =  .
.
Смешанное произведение имеет простое геометрическое толкование - это скаляр, по абсолютной величине равный объему параллелепипеда, построенного на трех данных векторах.
Если векторы образуют правую тройку, то их смешанное произведение есть число положительное, равное указанному объему; если же тройка a, b, c - левая, то a b c <0 и V = - a b c , следовательно V = êa b c ê.
Координаты векторов, встречающиеся в задачах первой главы, предполагаются заданными относительно правого ортонормированного базиса. Единичный вектор, сонаправленный вектору а, обозначается символом а о . Символом r =ОМ обозначается радиус-вектор точки М, символами а, АВ или êа ê, êАВ ê обозначаются модули векторов а и АВ.
Пример 1.1 . Зная векторы a и b, на которых построен параллелограмм, выразить через них вектор, совпадающий с высотой параллелограмма, перпендикулярной к стороне a .
Решение. Обозначим AB =a, AC =b , CD =h , где CD ^a , D-основание перпендикуляра, опущенного из точки C на сторону a. По правилу сложения векторов имеем: b + h = AD , h = AD - b. Поскольку AD çç a , то AD = l a .
Найдем значение l, используя ортогональность векторов a и h : ah =0 или a (l a-b )= 0, откуда l = ab /a 2 . Следовательно, h = (ab /a 2 ) a - b .
А B![]()
![]()

![]()

b h a
C D
Рис. 1
Пример 1.2. Найдите угол между векторами a = 2m +4n и b = m-n , где m и n - единичные векторы и угол между m и n равен 120о .
Решение . Имеем: cos j = ab /ab, ab = (2m +4n ) (m-n ) = 2 m 2 - 4n 2 +2mn = = 2 - 4+2cos120o = - 2 + 2(-0.5) = -3; a = ![]() ; a 2 = (2m +4n ) (2m +4n ) = = 4 m 2 +16mn +16 n 2 = 4+16(-0.5)+16=12, значит a =
; a 2 = (2m +4n ) (2m +4n ) = = 4 m 2 +16mn +16 n 2 = 4+16(-0.5)+16=12, значит a = ![]() . b =
. b = ![]() ; b 2 = = (m-n )(m-n ) = m 2 -2mn + n 2 = 1-2(-0.5)+1 = 3, значит b =
; b 2 = = (m-n )(m-n ) = m 2 -2mn + n 2 = 1-2(-0.5)+1 = 3, значит b = ![]() . Окончательно имеем: cos j =
. Окончательно имеем: cos j =![]() = -1/2, Þ j = 120o .
= -1/2, Þ j = 120o .
Пример 1.3. Зная векторы AB (-3,-2,6) и BC (-2,4,4),вычислите длину высоты AD треугольника ABC.
Решение . Обозначая площадь треугольника ABC через S, получим: S = 1/2 BC AD. Тогда AD=2S/BC, BC= ![]() =
=![]() = 6, S = 1/2 çAB ´ AC ç . AC=AB+BC , значит, вектор AC имеет координаты AC (-5,2,10). AB ´ AC =
= 6, S = 1/2 çAB ´ AC ç . AC=AB+BC , значит, вектор AC имеет координаты AC (-5,2,10). AB ´ AC = 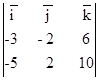 = i (-20 -12) - j (30 -30) + k (- 6 - 10) = = -16(2`i +`k ). çAB ´ AC ç =
= i (-20 -12) - j (30 -30) + k (- 6 - 10) = = -16(2`i +`k ). çAB ´ AC ç = ![]() = 16
= 16![]() ; S = 8
; S = 8![]() , откуда AD =
, откуда AD = ![]() =
=![]() .
.
Пример 1.4 . Даны два вектора a (11,10,2) и b (4,0,3). Найдите единичный вектор c, ортогональный векторам a и b и направленный так, чтобы упорядоченная тройка векторов a, b, c была правой.
Решение. Обозначим координаты вектора c относительно данного правого ортонормированного базиса через x, y, z.
Поскольку c ^ a, c ^ b , то ca = 0, cb = 0. По условию задачи требуется, чтобы c = 1 и a b c >0.
Имеем систему уравнений для нахождения x,y,z: 11x +10y + 2z = 0, 4x+3z=0, x2 + y2 + z2 = 0.
Из первого и второго уравнений системы получим z = -4/3 x, y = -5/6 x. Подставляя y и z в третье уравнение, будем иметь: x2 = 36/125, откуда x = ± ![]() . Используя условие a b c > 0, получим неравенство
. Используя условие a b c > 0, получим неравенство
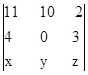 > 0 или 5(6x-5y-8z) > 0.
> 0 или 5(6x-5y-8z) > 0.
С учетом выражений для z и y перепишем полученное неравенство в виде: 625/6 x > 0, откуда следует, что x>0. Итак, x = ![]() , y = -
, y = -![]() , z =-
, z =-![]() .
.
2. Линии на плоскости
При чтении экономической литературы приходится иметь дело с большим количеством графиков. Укажем некоторые из них.
Кривая безразличия - кривая, показывающая различные комбинации двух продуктов, имеющих одинаковое потребительское значение, или полезность, для потребителя.
Кривая потребительского бюджета - кривая, показывающая различные комбинации количеств двух товаров, которые потребитель может купить при данном уровне его денежного дохода.
Кривая производственных возможностей - кривая, показывающая различные комбинации двух товаров или услуг, которые могут быть произведены в условиях полной занятости и полного объема производства в экономике с постоянными запасами ресурсов и неизменной технологией.
Кривая инвестиционного спроса - кривая, показывающая динамику процентной ставки и объем инвестиций при разных процентных ставках.