Дипломная работа: Высшая математика для менеджеров

tg j = .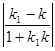

Равенство 1 + k₁ k = 0 есть необходимое и достаточное условие перпендикулярности прямых.

Для того, чтобы два уравнения

A₁ x + B₁ y + C₁ = 0, (2.7)

A₂ x + B₂ y + C₂ = 0, (2.8)

задавали одну и ту же прямую, необходимо и достаточно, чтобы их коэффициенты были пропорциональны:

A₁ /A₂ = B₁ /B₂ = C₁ /C_2.

Уравнения (2.7), (2.8) задают две различные параллельные прямые, если A₁ /A₂ = B₁ /B₂ и B₁ /B₂ ¹ C₁ /C_2; прямые пересекаются, если A₁ /A₂ ¹ B₁ /B₂ .

Расстояние d от точки M_о (x_о , y_о ) до прямой есть длина перпендикуляра, проведенного из точки M_о к прямой. Если прямая задана нормальным уравнением, то d = êr _о n ^о - р ê, где r _о - радиус-вектор точки M_о или, в координатной форме, d = êx_о cosa + y_о sina - р ê.

Общее уравнение кривой второго порядка имеет вид:

a₁₁ x² + 2a₁₂ xy + a₂₂ y² + 2a₁ x +2a₂ y +a = 0.

Предполагается, что среди коэффициентов a₁₁ , a₁₂ , a₂₂ есть отличные от нуля.

Уравнение окружности с центром в точке С(a, b) и радиусом, равным R:

(x - a)² + (y - b)² = R² . (2.9)

Эллипсом называется геометрическое место точек, сумма расстояний которых от двух данных точек F₁ и F₂ (фокусов) есть величина постоянная, равная 2a.

Каноническое (простейшее) уравнение эллипса:

x² /a² + y² /a² = 1. (2.10)

Эллипс, заданный уравнением (2.10), симметричен относительно осей координат. Параметры a и b называются полуосями эллипса.

Пусть a>b, тогда фокусы F₁ и F₂ находятся на оси Оx на расстоянии c= от начала координат. Отношение c/a = e < 1 называется эксцентриситетом эллипса. Расстояния от точки M(x, y) эллипса до его фокусов (фокальные радиусы-векторы) определяются формулами:

r₁ = a - ex, r₂ = a +ex.

Если же a < b, то фокусы находятся на оси Оy, c=, e = c/b, r₁ = b + ex, r₂ = b - ex.

Если a = b, то эллипс является окружностью с центром в начале координат радиуса a .

Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек F₁ и F₂ (фокусов) равна по абсолютной величине данному числу 2a.

Каноническое уравнение гиперболы:

x² /a² - y² /b² = 1. (2.11)

Гипербола, заданная уравнением (2.11), симметрична относительно осей координат. Она пересекает ось Оx в точках A (a,0) и A (-a,0) - вершинах гиперболы и не пересекает ось Оy. Параметр a называется вещественной полуосью , b - мнимой полуосью . Параметр c= есть расстояние от фокуса до начала координат. Отношение c/a = e >1 называется эксцентриситетом гиперболы. Прямые y = ± b/a x называются асимптотами гиперболы. Расстояния от точки M(x,y) гиперболы до ее фокусов (фокальные радиусы-векторы) определяются формулами:

r₁ = êex - a ê, r₂ = êex + a ê.

Гипербола, у которой a = b, называется равносторонней , ее уравнение x² - y² = a ² , а уравнение асимптот y = ± x. Гиперболы x² /a² - y² /b² = 1 и y² /b² - x² /a² = 1 называются сопряженными .

Параболой называется геометрическое место точек, одинаково удаленных от данной точки (фокуса) и данной прямой (директрисы).