Доклад: Сопряженная однородная задача

1. Сопряженный оператор.

2. Сопряженная однородная задача.

3. Условия разрешимости.

Сопряженный оператор.

Обозначим через дифференциальный оператор второго порядка, т.е.

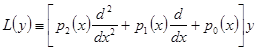(1)

где представляют собой непрерывные функции в промежутке . Если и - дважды непрерывно дифференцируемые на функции, то имеем:

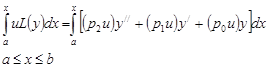(2)

Как и в предыдущем параграфе, интегрирование соотношения (2) по частям дает:

(3)

Обозначим дифференциальный оператор, входящий в подынтегральное выражение в правой части (3) через , т.е. (4)

При этом соотношение (3) перепишется так:

(5)

Оператор называется сопряженным по отношению к оператору . Умножая соотношение (4) на и интегрируя полученный результат по частям, по отношению к оператору . Таким образом, операторы и взаимно сопряжены.

Как и в предыдущем параграфе, дифференциальное уравнение:

(6)

будем называть сопряженным дифференциальному уравнению:

(7)

Если же , то оператор и дифференциальное уравнение будем называть сопряженными. Сравнивая выражения (1) и (5), приходим к выводу, что тогда и только, когда:

Таким образом, оператор будем самосопряженным тогда и только тогда, когда .

При этом:

Так как любое дифференциальное уравнение вида (7) можно преобразовать в самосопряженную форму, умножив на функцию .

Дифференцируя соотношение (5) по , получаем так называемую формулу Лагранжа:

(8)

Правая часть этой формулы может быть записана как:

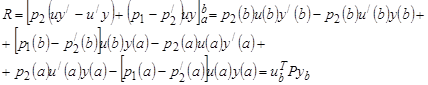(9)

где

(10)

--> ЧИТАТЬ ПОЛНОСТЬЮ <--