Книга: Машинна імітація випадкових параметрів

Точність оцінки математичного сподівання e = 0,022 для такого від­носно невеликого числа випробувань вважається задовільною. Звідси мож­на дійти висновку, шо перевірений генератор випадкових чисел придатний для розв'язування задач методом Монте-Карло.

Завдання

1. Выполнить проверку правильности генерации случайных чисел по тесту "Перевірка за моментами розподілу". Результаты поместить в таблицу следующего вида. Проанализировать результаты. Сделать выводы.

Количество испытаний	Мультипликативно - конгруэнтный метод		Смешанный генератор Томсона
	Математическое ожидание	Дисперсия	Математическое ожидание	Дисперсия
10
50
100
200
300

3.

4.Выполнить проверку правильности генерации случайных чисел по тесту "Перевірка на рівномірність за гистограмою". Создать две гистограммы распределения РВП: для мультипликативно - конгруэнтного метода и для смешанного генератора Томсона.

Перед построением диаграмм рекомендуется создать две таблицы следующего вида.

Мультипликативно - конгруэнтный метод		Смешанный генератор Томсона
Карманы	Частота	Карманы	Частота
0,05	0,05
0,10	0,10
0,15	0,15
0,20	0,20
0,25	0,25
0,30	0,30
0,35	0,35
0,40	0,40
0,45	0,45
0,50	0,50
0,55	0,55
0,60	0,60
0,65	0,65
0,70	0,70
0,75	0,75
0,80	0,80
0,85	0,85
0,90	0,90
0,95	0,95
1,00	1,00

Рекомендуется следующее оформление диаграммы.

5.Выполнить проверку правильности генерации случайных чисел также по гистограмме, используя программу на языке Паскаль (Смотри Приложение 1).

С помощью программы построить три гистограммы. Проанилизировать результаты. Сделать выводы.

В отчет скопировать гистограммы и текст программы.

Приклади використання методу Монте Карло в имитационном моделировании

Цель работы - ознакомление с возможностями практического применения метода Монте-Карло (1949) – численного метода моделирования случайных величин.

Для примера взяты две задачи: вычисление числа p и вычисление определённого интеграла.

Обчислення числа p

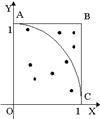
Расчёт числа p проводится путём набрасывания случайных чисел на квадрат со сторонами равными 1, в который вписана единичная окружность. Общее число случайных точек (на отрезке [0;1) принимается за N, а число точек, попавших в круг – за М.

Число p рассчитывается как:

Чем больше проводится экспериментов, тем точнее получается результат.

Практическое задание

Провести моделирование с целью исследования зависимости точности вычисляемого значения p от числа испытаний N.

Для моделирования разработать программное средство. Провести моделирование и результаты внести в таблицу. Проанализировать результат. Сделать выводы.

N	10	50	100	150	200
p

Для проведения моделирования студент должен создать программу на любом из алгоритмических языков или создать электроннную таблицу. Ниже предлагается один из возможных вариантов решения задачи в табличном процессоре. таблицу отформатировать. Снабдить комментариями.

X	Y	X^2+Y^2	Попадание в круг (1 или 0)	Приближенное значение числа p
4*M/N
Вычисление количества испытаний (N)	Вычисление суммы попаданий (M)

Обчислення визначенного інтегралу методом Монте-Карло

Вычисление определенного интеграла вида

производится по приближенной формуле:

,

где x_i - случайная величина, x_i =p/2×g, 0<=g<=1.

Точность результата также зависит от количества испытаний