Книга: Побудова простих великих чисел

Доведення. Нехай – складене й – нетривіальний простий дільник числа . Зазначимо, що завжди можна вибрати дільник так, що . Тоді з умови теореми випливає, що для всіх простих дільників числа існує ціле таке, що й .

Міркуючи аналогічно зауваженню до теореми Люка, отримуємо, що має знайтися елемент, який має порядок рівний за модулем . У силу малої теореми Ферма . Отже, справедливий ланцюжок нерівностей

.

Але , протиріччя.

Дана теорема показує, що якщо вдалося частково факторизувати число , причому факторизована частина задовольняє умову , то – просте.

Перш ніж переходити до подальшого, приведемо дві класичні частки випадку даної теореми.

Теорема 5. (Прот, 1878). Нехай , де .

Якщо існує число , для якого виконується умова

,

то – просте.

Теорема 6. (Прот, 1878). Нехай , де , і 3 не ділить . Тоді просте в тому і тільки в тому випадку, коли виконується умова

.

Доведення. У силу теореми Поклінгтона достатньо перевірити умову при й . Оскільки за умовою , то умова рівносильна виконанню рівності

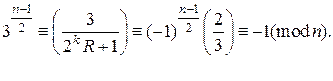
Зазаначимо, що якщо в теоремі Поклінгтона замінити рівність на більш слабку умову, то можна отримати
наступний результат.

Лема 1. Нехай , де – просте число, що не є дільником. Якщо існує ціле таке, що й , то знайдеться простий дільник числа виду при якомусь .

Доведення. Нехай . Тоді за умовою теореми в силу китайської теореми про залишки випливає, що існує таке , що й. Звідси отримуємо, що порядок елемента за модулем задовольняє умови: і не ділить. Тому.

У силу леми Гаусса про циклічність мультиплікативної групи кільця одержуємо. Зазначимо, що числа й взаємно прості як дільники сусідніх чисел. Тому. Отже,.

Хоча цей результат слабкіше, ніж теорема Поклінгтона, даний підхід, як показав Н. Дієметко в 1988 р., також може бути ефективно використаний для доведення простоти чисел.

Теорема (Дієметко). Нехай , де – просте, – парне й Якщо існує ціле таке, що й , то – просте.

Доведення. Нехай – не просте й . Тоді за лемою отримуємо, що існує таке , що.

Позначимо Тоді , де й . Звідси . Отже, , де – не може дорівнювати 0, інакше – просте, або 1, тому що – непарне. Аналогічно,. Таким чином,

.

Протиріччя. Теорему доведено.

Зазаначимо, що за умовою теореми числа й можуть бути не взаємно прості. Ця теорема лежить в основі алгоритму генерації простих чисел у вітчизняному стандарті на цифровий підпис Р 34.10-94.

У ньому як обираються не дуже високі степені числа 2, а перебуває перебором. (З 1 липня 2002 р. цей стандарт був замінений на новий Р 34.10-2001).

Метод Маурера

В 1995 р. У. Маурер опублікував швидкий алгоритм генерації доведених простих чисел, близьких до випадкового. У його основі лежить посилення теореми Поклінгтона на випадок, коли факторизована частина числа задовольняє нерівності . Крім того, йому вдалося оцінити ймовірність успіху при випадковому пошуку числа в умові теореми Поклінгтона.