Книга: Побудова простих великих чисел

Лема 2. Нехай Якщо існує ціле таке, що для будь-якого простого дільника числа виконані умови і , те кожен простий дільник числа має вигляд при деякому цілому Якщо, крім того, або – парне й , то – просте.

Доведення. Нехай – складене й – нетривіальний простий дільник числа . Тоді за умови теореми випливає, що й . Міркуючи аналогічно зауваженню до теореми Люка, отримуємо, що має знайтися елемент, який має порядок рівний за модулем . У силу малої теореми Ферма .

Для доведення другого твердження, припустимо, що . Тоді .
Якщо , то Якщо - непарне й , то й

просте число поклінгтон мауер люк

Протиріччя.

Наступна лема доведена Д. Коувером і Дж. Куіскуотером в 1992 р.

Лема 3. Нехай і задовольняють умову леми 1. Визначимо числа й рівністю . Якщо й число не дорівнює нулю й не є повним квадратом, то - прості.

Доведення. Відповідно до леми 1 для кожного простого дільника числа виконується нерівність За умовою . Тому, якщо число

– складене, то воно не може мати більше двох простих дільників. Нехай

и. .

Маємо інакше .

Якщо , то

Звідси , однак у цьому випадку Тому .

Отже, і . За теоремою Вієта є коренями квадратного рівняння , що має розв’язання в цілих числах у тому і тільки в тому випадку, якщо є повним квадратом або нулем. Лему доведено.

Зазначимо, що переконатися, що задане число не є повним квадратом, можна, обчисливши символ Лежандра для декількох маленьких простих модулів. Якщо при деякому модулі число не буде квадратичним відрахуванням, то воно не буде й повним квадратом.

Нехай – функція Ейлера.

Лема 4. Нехай – просте число й . Позначимо через число елементів , порядок яких ділиться на . Тоді справедлива оцінка

,

причому рівність виконується в тому й у тільки в тому випадку, коли

Доведення. Використовуючи властивості функції Ейлера, отримуємо

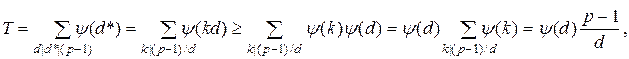
причому рівність виконана в тому і тільки в тому випадку, коли