Контрольная работа: Абсолютні і відносні величини зведення і груповання статистичних даних ряди розподілу

3,48

Частота 6 10 9 25

Середня величина розраховується як середнє зважене за формулою:

,

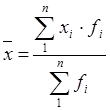де x_i – і-та варіанта (середина і-го інтервалу), f_i – частота і-го інтервалу, n – число груп (інтервалів).

Середня величина капіталу:

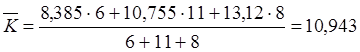
середня прибутковість активів

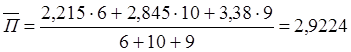
Для знаходження моди спочатку знаходимо модальний інтервал – тобто інтервал, який має найбільшу частоту.

Модальний інтервал розподілу банків за розміром капіталу – це інтервал [9,57 – 11,94), який містить 11 елементів.

Модальний інтервал для розподілу у банків за прибутковістю активів – це інтервал [2,53, 3,16), який містить 10 елементів.

Мода Мо розраховується за формулою:

,

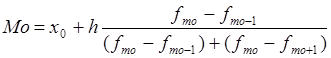де x₀ та h – нижня межа та ширина модального інтервалу відповідно,

f_mo , f_mo-1 , f_mo+1 –частоти (частки) відповідно модального, передмодального і післямодального інтервалу.)

Моду розподілу банків за розміром капіталу Мо_К знаходимо, підставляючи чисельні значення x₀ = 9,57; h =2,53; f_mo = 11; f_mo-1 = 6; f_mo+1 = 8:

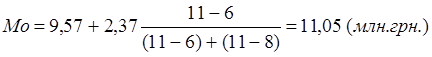
Моду розподілу банків за прибутковістю активів Мо_А знаходимо, підставляючи чисельні значення x₀ = 2,53; h =0,63; f_mo = 10; f_mo-1 = 6; f_mo+1 = 9:

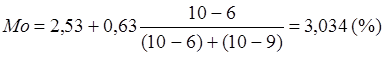
Медіана Ме розподілу, поданого інтервал ним варіаційним рядом, визначається за інтерполяційною формулою

,

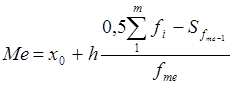де x₀ та h – нижня межа та ширина модального інтервалу відповідно,

f_mе –частота медіанного інтервалу,

– кумулятивна частота передмедіанного інтервалу.

Медіану розподілу банків за розміром капіталу Ме_К знаходимо, підставляючи чисельні значення x₀ = 9,57; h =2,37; , f_me =11:

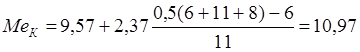
Медіану розподілу банків за прибутковістю активів Ме_А знаходимо, підставляючи чисельні значення x₀ = 2,53; h =,63; , f_me =10:

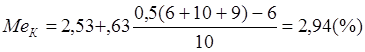
Середнє лінійне відхилення розраховується як середнє абсолютних значень відхилень від середнього вибіркового за формулою