Контрольная работа: Аналіз стійкості процесів в нелінійній схемі

Так, як же повинні бути зв’язані ці дві задачі – розрахунок періодичного режиму та аналіз його стійкості? Щоб зрозуміти цей зв’язок скористаємось спектральним уявленням.

Припустимо, періодичний режим розраховується часовим методом. Тоді, на спектральний склад усталеного процесу обмеження не накладаються. Тому можна казати, що враховано багато гармонік (можливо нескінченна кількість). Цю обставину і треба мати на увазі при обранні методу дослідження стійкості: при аналізі повинно враховуватися багато гармонік. Очевидно підходять обидва розібрані вище методи, які опираються на характеристичну матрицю і нескінченний визначник Хіла.

Зараз припустимо, що періодичний режим був знайдений спектральним методом і було взято до уваги N гармонік. Нехай результати обліку ще однієї гармоніки практично співпали з попередніми. Це означає, що на лінійну частину схеми повинні бути накладені певні вимоги. Провідність на частотах вище повинна практично замикати затискачі, до яких ввімкнені нелінійні елементи. Якщо така вимога не виконується, то результати двох останніх розрахунків, про які мовилося вище, будуть відрізнятися один від одного. Таким чином, коли періодичний режим розраховано із врахуванням гармонік і його результати припускаються достовірними, то модуль опору лінійної частини схеми на частотах, вище

( - період розглядаємого режиму), дорівнює нулю або нескінченно великий. Цей факт і повинен лягти в основу обрання методу аналізу стійкості. Мабуть, в цьому випадку доцільно скористатися скінченим визначником Хіла, зберігаючи в ньому відповідне число рядків та стовпців.

стійкість рівновага періодичний режим

5. Аналіз стійкості періодичного режиму, отриманого часовим методом

Як вказувалося, в цій ситуації, щоб аналізувати стійкість, треба розраховувати характеристичну матрицю, або використовувати нескінченний визначник Хіла.

Шуканими даними для обчислення елементів характеристичної матриці є еквівалентна схема для малих збурень, в якій закон зміни параметрів кожного моделюючого елемента повинен бути задано, як функція часу. Подальша послідовність розрахунків така:

- складання диференційного рівняння схеми для малих збурень;

- n-кратне інтегрування цих рівнянь (n – порядок схеми) на протязі періоду модуляції при початкових умовах, заданих стовпцем одиничної матриці; це дозволяє сформувати характеристичну матрицю, так як після кожного інтегрування знаходимо значення змінних при , що дає один стовпець матриці;

- розрахунок власних значень характеристичної матриці.

При другому методі використовується вираз, до якого приводиться нескінченний визначник. Якщо мати на увазі рівняння для малих збурень (9), то значення характеристичних показників потрібно знаходити за допомогою формули (12), прийнявши рівною нулю її праву частину.

Рішення рівняння, в якому невідоме входить як співмножник до аргументу тригонометричних функцій, надто складне. Позначивши , отримаємо

,

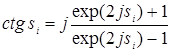причому .

В результаті

,

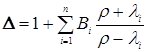де .

Після приведення до загального знаменника знайдемо

. (14)

Поліном чисельника є характеристичним для рівняння (9), так його корені, зв’язані відповідним чином із характеристичними показниками, перетворюють в нуль визначник Хіла. Корені полінома знаменника є “мультиплікаторами” усередненої системи. Ступінь обох поліномів однакова. Коефіцієнти характеристичного полінома визначаються через “мультиплікатори” усередненої системи. Наприклад,

.

Формули для інших коефіцієнтів набагато складніші.

Таким чином, за допомогою нескінченного визначника Хіла маємо змогу знайти характеристичний поліном рівняння для малих збурень без інтегрування самого рівняння.

Аналіз стійкості із використанням нескінченного визначника Хіла можна зробити двома способами. Перший зводиться до обчислення коефіцієнтів характеристичного полінома. Другий заснований на вивченні годографа визначника при та зміні частоти.

1. Опишемо перший алгоритм розглянутого методу. Шукані дані ті ж, що і в попередньому методі. Але для модульованих елементів повинні бути відомі коефіцієнти рядів Фур’є. Послідовність розрахунків виглядає так:

- обчислення - характеристичних коренів усередненої системи;

- n-кратний розрахунок елементів чисельного визначника при та розрахунок за допомогою формули (13);

- розрахунок коефіцієнтів характеристичного полінома;