Контрольная работа: Аппроксимация функций 2

end

x=sum(Pn,2);

_____________________________________________________________

i=0;

for p=11:0.05:12

i=i+1;

a=0.5+i*0.5;

x1(i)=p;

ff(i)=Nuton_nz(a,x,y);

end

% Построениеграфика

subplot(2,1,2); plot(x1,ff,'.-'); ylabel('y'); xlabel('x'); grid on

title('Интерполяция многочленом Ньютона назад')

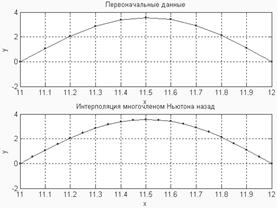
Рис. 4. Интерполяция многочленом Ньютона назад

4. Квадратичная сплайн-интерполяция

Для того, чтобы выполнить квадратичную сплайн-интерполяцию по 6-ти узлам, необходимо задаться пятью уравнениями.

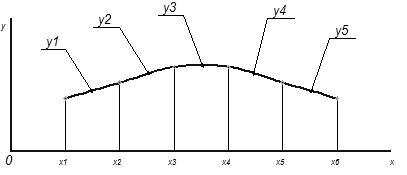
Рис. 5. К выводу коэффициентов при сплайн-интерполяции

При квадратичном сплайне уравнения будут иметь вид:

, .

На эти уравнения наложены следующие граничные условия:

, , , .

Вычислим производную

: , . (1)

Определим при : , . (2)

В рассматриваемом примере . С учетом этого, а также с учетом выражения (2) и условия , запишем следующую зависимость:

, .

Из условия и выражения (1) получим: .