Контрольная работа: Автоматизация системного проектирования
Симплекс-метод был разработан и впервые применен для решения задач в 1947 г. американским математиком Дж. Данцигом. Симплекс метод принадлежит к числу аналитических методов решения основной задачи линейного программирования.
Составим линейные уравнения для решения задачи.
F (x) = 6х1 + 6 х2 →max – целевая функция.
где х1 – количество изделий Р1;
х2 - количество изделий Р2.
Уравнения ограничений :
4 х1 ≤ 20;
х1 + 2 х2 ≤ 37;
х1 + 4 х2 ≤ 40.
Найдем наибольшее значение линейной функции
F= 6 x1 + 6 x2
при следующих ограничениях
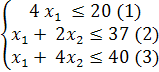
Нам необходимо найти начальное опорное ( абсолютно произвольное ) решение для исходной функции, которое бы удовлетворяло системе наложенных ограничений. Далее, применяя симплекс таблицы, мы будем получать решения, при которых значение функции будет, как минимум, не убывать. И так до тех пор, пока не достигнем оптимально решения, при котором функция достигает своего максимума. Если, конечно, рассматриваемая нами линейная функция обладаем максимальным значением при заданной системе ограничений. Перед применением симплекс таблиц, необходимо преобразовать систему линейных ограничений и рассматриваемую нами функцию к вполне определенному виду.
Свободные члены системы ограничений положительны. Выполнено одно из необходимых условий применения симплекс метода.
К левой части неравенства 1 системы ограничений прибавляем неотрицательную переменную x3 , тем самым мы преобразуем неравенство 1 в равенство.
К левой части неравенства 2 системы ограничений прибавляем неотрицательную переменную x4 , тем самым мы преобразуем неравенство 2 в равенство.
К левой части неравенства 3 системы ограничений прибавляем неотрицательную переменную x5 , тем самым мы преобразуем неравенство 3 в равенство.
Введенные нами переменные имеют вполне конкретный физический смысл, непосредственно связанный с условием нашей задачи.
4 x1 + x3 = 20
x1 + 2 x2 + x4 = 37
x1 + 4 x2 + x5 = 40
Система ограничений приведена к каноническому виду, т.е все условия системы представляют собой уравнения. Выполнено еще одно из необходимых условий применения симплекс метода.
Определимся с начальным опорным решением. Наличие единичного базиса в системе ограничений позволяет легко найти начальное опорное решение. Рассмотрим подробнее.
Переменная x3 входит в уравнение 1 с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е x3 - базисная переменная.
Переменная x4 входит в уравнение 2 с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е x4 - базисная переменная.
Переменная x5 входит в уравнение 3 с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е x5 - базисная переменная.
Переменные , которые не являются базисными называются свободными переменными. Приравняв свободные переменные нулю в получившийся системе ограничений мы получим начальное опорное решение.
X нач = ( 0 , 0 , 20 , 37 , 40 )