Контрольная работа: Дедуктивні умовиводи

На обвинувачуваного (М) не може бути покладено обов'язокдоведення своєї невинності (Р).

Петренко (S) — обвинувачуваний у справі (М).

Отже, на Петренка (S) не може бути покладено обов'язокдоведення своєї невинності (Р).

Наявність у силогізмі одного заперечного засновку означає, ще обсяг середнього терміна виключається із обсягу одного з крайніх термінів. Тоді з обсягу одного крайнього терміна буде виключатися обсяг другого крайнього терміна, котрий входить до обсягу середнього терміна. У нашому прикладі обсяг М виключається із обсягу Р. Отже, і обсяг S, котрий становить частину обсягу М, неодмінно виключається ізобсягу Р (мал. 8). Тому висновок може бути тільки заперечним, а не ствердним.

6. Із двох часткових засновків не можна зробити ніякого висновку.

Це правило випливає з інших перелічених намиправил.

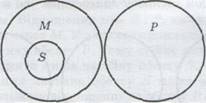
мал. 8

Якщо обидва засновки є частковоствердними, то з них неможна зробити істинного висновку тому, що в жодному засновку не буде розподіленого середнього терміна.

Якщо ж один частковий засновок ствердний, а другийчастковий засновок, у котрому М займає місце предиката, заперечний (тоді середній термін буде розподіленим), то в силогізмі порушується третє правило: термін, нерозподілений узасновку, стає розподіленим у висновку.

7. Якщо один із засновків частковий, то й висновок маєбути частковим. Це правило забороняє робити загальні висновки, коли один із засновків силогізму є судженням частковим.

За одного часткового засновку середній термін відноситьсялише до частини обсягу меншого терміна, а не до всього йогообсягу. Тому з обсягом Р пов'язується не увесь обсяг S, а тільки та його частина, котру займає М. Тоді й у висновку ми можемо говорити тільки про деякі S, а не про всі.

Наприклад:

Деякі громадяни (М) не є дієздатними (Р).

Кожен громадянин (М) є правоздатним (S).

Отже, деякі правоздатні (S) не є дієздатними (Р).

Коли б із цих засновків ми зробили загальний висновок "Усі правоздатні не є дієздатними", то він був би хибним. У цьому неважко переконатися, відобразивши силогізм колами (мал. 9).

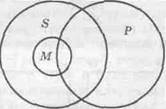
мал. 9

1.5 Фігури категоричного силогізму

Категоричний силогізм має різні види, котрі набули назви фігур силогізму.

Фігурами силогізму називаються форми силогізму, що відрізняються одна від одної розташуванням середнього терміна в засновках. Існує чотири фігури силогізму.

У першій фігурі середній термін займає місце суб'єкта у більшому засновку і предиката — в меншому. Схема першої фігури:

М - Р

S -М

S - Р.

У другій фігурі середній термін займає місце предиката в обох засновках. Схема другої фігури:

P - M

S – M

S – P