Контрольная работа: Дедуктивные умозаключения
Рис. 1
Истинность импликации (столбик 3) зависит от истинности антецедента (основания) (1) и консеквента (следствия) (2). Импликация считается ложной тогда и только тогда, когда антецедент истинен, а консеквент ложен (2-я строка таблицы). Во всех остальных случаях импликация истинна. Истинность или ложность конъюнкции (4-й столбик) также зависит от составляющих ее членов (3 и 1).
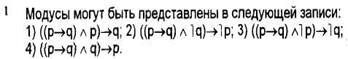
Конъюнкция истинна тогда и только тогда, когда истинны оба ее члена (1-я строка таблицы).
Теперь установим истинность импликации (5-й столбик таблицы — утверждающий модус). Так как импликация антецедента (4) и консеквента (2) не содержит случая, когда антецедент истинен, а консеквент ложен, то импликация всегда истинна. Следовательно, высказывание ((р→q)![]() р)→q является логическим законом. Отрицающий модус (рис. 2).
р)→q является логическим законом. Отрицающий модус (рис. 2).
В столбиках 1 и 3, 2 и 4 показано, что если одно высказывание ложно, то его отрицание истинно. Импликация р и q (1 и 2) ложна только в одном случае (2-я строка таблицы) — столбик 5. Конъюнкция (столбик 6) высказываний (p → q) и ˉ|q (5 и 4) истинна только в одном случае (4-я строка таблицы). Импликация ((p→q) ![]() ˉ|q) и ˉ|р (6 и 3) всегда истинна, так как не содержит случая, когда антецедент истинен, а консеквент ложен. Следовательно, высказывание ((p→q)
ˉ|q) и ˉ|р (6 и 3) всегда истинна, так как не содержит случая, когда антецедент истинен, а консеквент ложен. Следовательно, высказывание ((p→q)![]() ˉ|q)→ˉ|p является логическим законом.
ˉ|q)→ˉ|p является логическим законом.
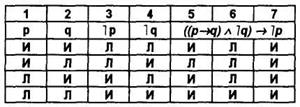
Рис. 2
С помощью таблиц истинности можно показать недостоверность выводов по неправильным модусам.
При анализе условно-категорического умозаключения нужно иметь в виду, что основание и следствие большей посылки может быть как утвердительным, так и отрицательным суждением: p→q; ˉ|p→q; p→ˉ|q; ˉ|p→ˉ|q. Например:

Следствие условной посылки — отрицательное суждение, категорическая посылка (утвердительное суждение) утверждает истинность основания, заключение (отрицательное суждение) утверждает истинность следствия.
В символической записи:
![]()
Возможны и другие разновидности модусов.
Иногда в рассуждениях используются условно-категорические умозаключения с выделяющим условным (эквивалентным) суждением (если, и только если а, то b).
В символической записи: p ![]() q, где
q, где ![]() — знак эквивалентности. В таких умозаключениях достоверные заключения получаются по всем четырем модусам:
— знак эквивалентности. В таких умозаключениях достоверные заключения получаются по всем четырем модусам:
![]()
Рассмотрим для примера выделяющее условное суждение: «Если лицо виновно в совершении преступления, то оно подлежит уголовной ответственности». Нетрудно установить, что достоверное заключение получается по любому из приведенных модусов.
Разделительно-категорическое умозаключение
Разделительно-категорическим называется умозаключение, в котором одна из посылок — разделительное, а другая посылка и заключение — категорические суждения.
Простые суждения, из которых состоит разделительное (дизъюнктивное) суждение, называются членами дизъюнкции или дизъюнктами. Например, разделительное суждение «Облигации могут быть предъявительскими или именными» состоит из двух суждений — дизъюнктов: «Облигации могут быть предъявительскими» и «Облигации могут быть именными», соединенных логическим союзом «или».
Утверждая один член дизъюнкции, мы с необходимостью должны отрицать другой, и отрицая один из них — утверждать другой. В соответствии с этим различают два модуса разделительно-категорического умозаключения: утверждающе-отрицающий и отрицающе-утверждающий.

Схема утверждающе-отрицающего модуса:
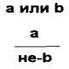
В утверждающе-отрицающем модусе (modus ponendo tollens) меньшая посылка — категорическое суждение — утверждает один член дизъюнкции, заключение — также категорическое суждение — отрицает другой ее член. Например:

Заключение по этому модусу всегда достоверно, если соблюдается правило: большая посылка должна быть исключающе-разделительным суждением, или суждением строгой дизъюнкции. Если это правило не соблюдается, достоверного заключения получить нельзя. В самом деле, из посылок «Кражу совершил К или Л» и «Кража совершена К» заключение «Л кражу не совершал» с необходимостью не следует. Возможно, что Л также причастен к совершению кражи, является соучастником К.