Контрольная работа: Дисперсія у одномодових телекомунікаційних волокнах
і взяти (11) для визначення характеристики чи рівняння власного значення для одержання постійної розповсюдження (blm взагалі для волокна з градiєнтною серцевиною поки задовольняється (7). Використовуючи (11), можна також зробити розрахунок числа мод, як показано в:
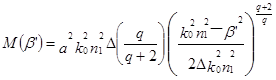 , (12)
, (12)
та
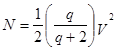 , (13)
, (13)
де M(b') представляє кількість мод, що мають постійні поширення більші, ніж b', та N відповідає загальній кількості можливих спрямованих мод. Для східчастого профіля волокна (q=¥)
![]() , (14)
, (14)
в той час як для волокна з параболічною серцевиною (q=2)
![]() . (15)
. (15)
Таким чином, для даного V загальна кількість спрямованих мод в волокні зі східчастим профiлем вдвічі більше, ніж в еквівалентному (що має з ним однакові (D та а) волокні з параболічним профілем. Звичайно V в багатомодових волокнах ~30, тоді при q=¥ N буде дорівнюватися »450, тоді як при q=2 N@225.
Встановлено, що в оптичних системах передачі з iмпульсно-кодовою модуляцією з-за того, що сигнал передається в формі серій iмпульсів, ці iмпульси розширюються при поширенні в середині волокна в основному з-за межмодової дисперсії і міра дисперсії буде визначати можливу швидкість передачi інформації (даних) через волокно. Реально, дисперсія чи поширення iмпульсу в волокні породжується, як це можна показати, трьома механізмами:
1) міжмодовою,
2) матеріальною,
3) хвильоводною дисперсією (останні дві разом відомі як внутрішньомодова або хроматична дисперсія). Навіть якщо шляхом підбору градiєнтного профіля можна мiнiмiзувати міжмодову дисперсію, кінцева спектральна ширина практично доступних оптичних джерел, як і Фур'є-спектр iмпульсних сигналів призведе до внутрішньомодової дисперсії. Матеріальна дисперсія, що є однією з компонент її, зобов'язана своєю появою залежності показника заломлення, з якого зроблено волокно, від довжини хвилі. З іншого боку, хвилєводна дисперсія виникає із-за явної залежності постійної розповсюдження моди від довжини хвилі і, по суті, залежить від хвилєводного параметру: a/l.
Якщо ми, наприклад, візьмемо поширення iмпульсу гаусовської форми:
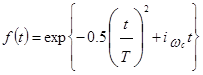 , (16)
, (16)
де Т – половина ширини iмпульсу на рівні інтенсивності 1/e та wс – частота несучої, тоді можливо показати після одержання Фур'є-спектра від f(t), що після поширення через довжину L волокна кожної p-ї моди, розподіл інтенсивності p- ї моди буде даватися як:
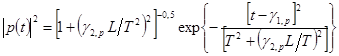 . (17)
. (17)
Тут індекс p для композиційної моди замінює номер двох індексів l і m, звичайно використовуваних для подання довільної моди, g1,p =gbp /dw½w = w c , g2,p =d2 bp /dw2 ½w = w c . Рівняння (17) показує, що, як і вхідний iмпульс, вихідний імпульс має також гаусову форму і половина ширини вихідного iмпульсу, відповідного p-й моді, більше, ніж вхідний iмпульс, стосовно до Т це:
![]() . (18)
. (18)
В дійсності, так як багатомодове волокно підтримує велику кількість мод, повна інтенсивність, що буде визначатися законом другого ступеня в приймачі на виході лінії, буде даватися виразом:
![]() , (19)
, (19)
де Ap – амплітудний коефіцієнт p-ї моди. Важлива деталь, яку треба визначити – те, що час затримки передачі чи групова затримка (tg ), зв'язана з кожною модою і, як очікувалося, дається як L dbp /dw і, крім того, міжмодова дисперсія приведе до різниці часу передачі між різноманітними модами. Понад того, спотворення форми iмпульсу в основному визначається другою похідною: d2 bp /dw2 .
Використовуючи (11) і (12), може бути показано, що
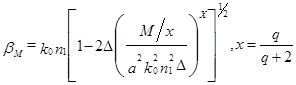 . (20)
. (20)
Прості дії сводять вираз до:
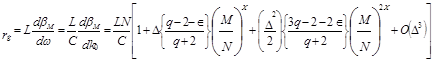 , (21)
, (21)
де 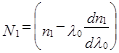 називається груповим індексом, l0 – довжина хвилі в свободному просторі і Î відоме як профіль дисперсійного параметра, що дається формулою:
називається груповим індексом, l0 – довжина хвилі в свободному просторі і Î відоме як профіль дисперсійного параметра, що дається формулою:
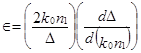 . (22)
. (22)
З (21) явно виходить, що для
q=2+κqopt , (23)