Контрольная работа: Длина дуги кривой в прямоугольных координатах

Положим теперь, что , тогда

.

Полученное выражение называется формулой Ньютона – Лейбница. Другая форма записи этого выражения следующая:

.

Обычно в полученных выражениях переменная интегрирования обозначается буквой .

Таким образом, чтобы вычислить определенный интеграл, необходимо найти любую первообразную от и вычислить разность ее значений в верхнем и нижнем пределах интегрирования. Полученная простая формула позволяет легко находить решения многих математических и прикладных задач, связанных с вычислением определенного интеграла.

3 . Замена переменной в определенном интеграле

При изучении неопределенного интеграла было показано (п. 5.4), что одним из наиболее часто встречающихся методов его вычисления является замена переменных. Так как вычисление определенного интеграла, согласно формуле Ньютона – Лейбница, также связано с нахождением первообразной, то метод замены переменной применим и в нем, однако при этом имеются некоторые особенности. В неопределенном интеграле замена переменной приводила в конце вычислений к обратной замене, в определенном же, оказывается, можно обойтись без этого.

Теорема. Если в определенном интеграле , где непрерывна на , сделать замену переменной и при этом:

1) , ;

2) и непрерывны на ;

3) непрерывна на и при изменении от до не выходит за пределы отрезка ,

то .

Пусть – какая-то первообразная от , тогда . Согласно формуле Ньютона – Лейбница, получим соответствующий определенный интеграл: . Но, как было показано в п. 5.4, в неопределенном интеграле можно сделать замену переменной , тогда . В этом случае соответствующий определенный интеграл будет иметь вид:

.

У обоих определенных интегралов правые части равны, следовательно, равны и левые части:

,

что и требовалось доказать.

Из доказанной теоремы следует, что при замене переменной в определенном интеграле должны поменяться пределы интегрирования, и обратная замена здесь уже не нужна, так как и при старой и при новой переменной в ответе получается одно и то же число.

4 . Интегрирование по частям в определенном интеграле

Пусть даны функции и , которые непрерывны со своими производными на . Составим их произведение и продифференцируем его:

.

Возьмем от обеих частей полученного равенства определенные интегралы:

.

Но 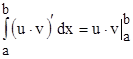, , . Следовательно, 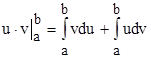, откуда: 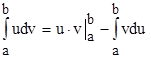. Так же как и в неопределенном интеграле, данная формула требует правильного выбора множителей и .

5 . Длина дуги кривой в прямоугольных координатах

При вычислении длины кривой линии может быть использована та же методика, что и при вычислении площадей криволинейных трапеций, то есть кривую разбивают на такие малые участки, длину которых можно посчитать геометрическими методами.

Определение. Длиной дуги кривой линии называют предел, к которому стремится длина вписанной в нее ломаной линии при неограниченном увеличении числа ее звеньев и при стремлении длины наибольшего звена к нулю .