Контрольная работа: Длина дуги кривой в прямоугольных координатах

Итак, пусть кривая линия описывается функцией на отрезке . При этом пусть непрерывна на этом отрезке вместе со своей производной . Разобьем кривую на частичных дуг точками . Соединив начало и конец каждой частичной дуги хордой, получим в результате вписанную ломаную линию, длина которой равна сумме длин ее звеньев:

.

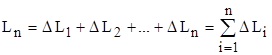Обозначим: , ,…, ,…, . Кроме того, , ,…, ,…, . В таком случае можно рассматривать как гипотенузу прямоугольного треугольника и поэтому

.

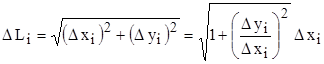Согласно теореме Лагранжа о среднем

, где ,

следовательно,

.

Отсюда длина ломаной линии равна

.

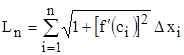Переходя к пределу в данной интегральной сумме, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю, получаем длину кривой линии в прямоугольной системе координат:

.

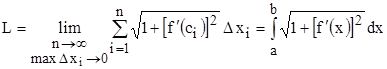Данный интеграл существует, поскольку по условию производная непрерывна.

Из полученной формулы можно получить выражение для дифференциала дуги, которое используется как в математике, так и в некоторых задачах теоретической механики. Пусть положение правого конца кривой линии является переменной величиной, тогда ее длина будет функцией точки, в которой она заканчивается, то есть

.

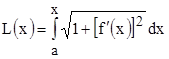Возьмем производную данного интеграла по переменному верхнему пределу (п. 1.):

.

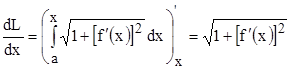Отсюда следует, что

.

6 . Длина дуги кривой при ее параметрическом задании

Рассмотрим теперь случай, когда кривая, длину которой необходимо вычислить, задана параметрически, то есть 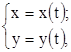при этом изменение от до приводит к изменению от до . Пусть функции и непрерывны вместе со своими производными на отрезке и при этом . Тогда , а . Подставим значение данной производной и дифференциала в формулу для длины дуги в прямоугольной системе координат (п. 5):

.

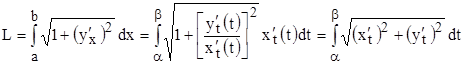В случае пространственной кривой ее параметрическое задание будет выглядеть следующим образом:

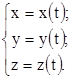
Если указанные функции непрерывны вместе со своими производными на отрезке , то можно доказать, что длина данной кривой вычисляется по формуле

.

7 . Длина дуги в полярной системе координат

Если кривая задана в полярной системе координат, то она описывается функцией , где . Пусть непрерывна вместе со своей производной на отрезке .

Перейдем от полярной к прямоугольной системе координат: . Но так как , то получаем, что . Иначе говоря, и выражены через параметр , поэтому можно воспользоваться формулой для длины дуги при ее параметрическом задании (п. 6.):