Контрольная работа: Элементы алгебры и геометрии

Первую строку умножим на 3 и вычтем из неё вторую, первую умножим на 5 и вычтем из неё третью:

Вычтем из второй строки – третью:

Ранг матрицы ![]()
Запишем расширенную матрицу 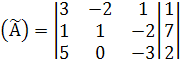
Найдем определитель расширенной матрицы. Поменяем местами первую и вторую строки:
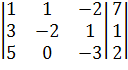
Умножим первую строку на 3 и вычтем из неё вторую, умножим первую строку на 5 и вычтем из неё третью:
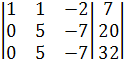
Вычтем из второй строки третью:
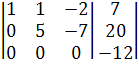
Ранг расширенной матрицы ![]()
Ранг расширенной матрицы системы не равен рангу матрицы системы, значит система несовместна (не имеет решений).
Задание № 54
Даны координаты точек А (х1 ;у1 ) и В (х2 ;у2 ) и радиус окружности R, центр которой находится в начале координат.
Требуется:
1) составить каноническое уравнение эллипса, проходящего через данные точки А и В;
2) найти полуоси, фокусы и эксцентриситет этого эллипса;
3) найти все точки пересечения эллипса с данной окружностью;
4) построить эллипс и окружность.
Решение:
1. Общий вид канонического уравнения эллипса:
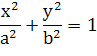
Подставим координаты точек А и В в общее уравнение:
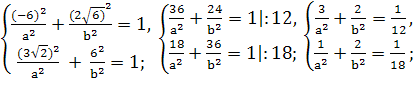
![]()
![]()