Контрольная работа: Энтропия сигналов
Объединение - совокупность двух и более ансамблей дискретных, случайных событий. С объединением связаны понятия условной, безусловной, совместной и взаимной энтропии.
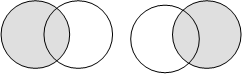
1. Безусловная энтропия - среднее количество информации, приходящееся на один символ (рис. 1). Если Х – передаваемое, а У - принимаемое сообщения, то можно записать следующие соотношения:
|
 X Y X Y
X Y X Y
Рис. 1. Безусловная энтропия
2. Условная энтропия - количество информации об источнике, когда известно, что принимается Y, или мера количества информации в приемнике когда известно, что передается X (рис. 2).
|
X Y X Y
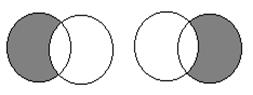
Рис. 2. Условная энтропия
3. Совместная энтропия - среднее количество информации на пару пе-реданных и принятых символов (рис. 3).
H(X,Y) = H(Y,X) = H(X)+H(Y/X)= H(Y)+H(X/Y)= H(X)+H(Y)-H(X×Y).
4. Взаимная энтропия - энтропия совместного появления статистически-зависимых сообщений (рис. 4).
H(X×?Y)=H(Y×X)=H(X)-H(X/Y)=H(Y)-H(Y/X)=H(X,Y)-H(X/Y)- H(Y/X).
X Y
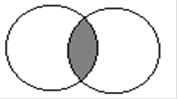
Рис. 3 Совместная энтропия
X Y

Рис. 4. Взаимная энтропия
На практике чаще всего встречаются взаимозависимые символы и сообщения. Например, при передаче текстовых сообщений передаются не просто буквы, а слова, имеющие определенные смысловые значения. При этом, каждая буква, и сочетание букв имеют различные вероятности появления в тексте. Условная энтропия учитывает взаимосвязь событий через их условные вероятности.
Рассмотрим схему рис. 5:
![]()
![]()
|
|
--> ЧИТАТЬ ПОЛНОСТЬЮ <--