Контрольная работа: Энтропия сигналов
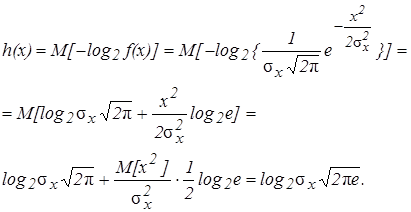
В соответствии с центральной предельной теоремой нормальным законам распределения подчиняются широкий класс, так называемых гауссовых случайных процессов или реальных сигналов.
Белый шум - помеха с наиболее ''зловредными" свойствами , т. е. передает максимальное количество вредящих сведений при заданной средней мощности и позволяет упростить расчеты для наихудшего случая.
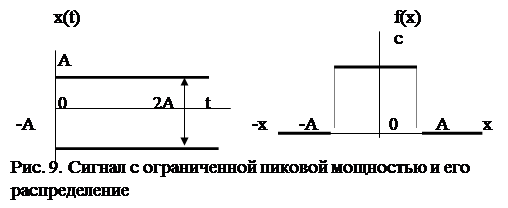
Для того чтобы сигнал с ограниченной пиковой мощностью имел максимальную информативность необходимо, чтобы он имел равномерное распределение (рис. 9). Определим дифференциальную энтропию для равномерного распределения, т. е. сигнала с ограниченной пиковой мощностью. Если P-пиковая мощность, то 
- максимальная амплитуда. Уравнение для дифференциальной энтропии с учетом ограничений имеет вид:
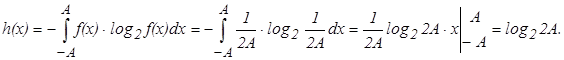
Дифференциальная энтропия для равномерного распределения равна:
(14)
 |
Полная энтропия сигнала с равномерным распределением равна:
, (15)
где m -число уровней квантования.
Определим дифференциальную энтропию для экспоненциального распределения. Это распределение широко используется для определения интенсивности отказов в радиоэлектронной аппаратуре
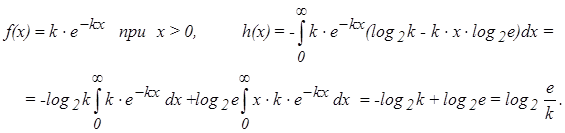
Полная энтропия для экспоненциального распределения равна:
. (16)
Список Литературы
1. Коганов А. В. Векторные меры сложности, энтропии, информации. “Математика. Компьютер. Образование”. Вып. 7, ч. 2, “Прогресс-Традиция”, М., 2000, с. 540 — 546
2. Яглом А. М., Яглом И. М. Вероятность и информация. М., 1957.
3. Шеннон К. Работы по теории информации и кибернетике. — М.: Изд. иностр. лит., 1963. — 830 с.
4. Волькенштейн М. В. Энтропия и информация. — М.: Наука, 1986. — 192 с.
5. Цымбал В. П. Теория информации и кодирование. — М.: Выща Школа, 1977. — 288 с.
6. Вероятностные методы в вычислительной технике. /Под ред. А.Н. Лебедева, Е.А.Чернявского. –М.: Высш. шк., 1986.
7. Седов Е.А. Взаимосвязь информации, энергии и физической энтропии в процессах управления и самоорганизации. Информация и управление. М., Наука, 1986.