Контрольная работа: Энтропия сигналов

f(x)

f(x_i )

0 D x x_i x

Рис. 6. График функции плотности вероятности

При этом, выражение для энтропии можно представить в виде

(9)

Переходим к пределу:

.

Полная энтропия источника непрерывных сообщений состоит из двух слагаемых, одно из которых определяется законом распределения, а второе является постоянной величиной, определяющей шаг квантования, который влияет на точность измерений. Этот член выражения определяет постоянную составляющую и исключается из рассмотрения.

Значение первого слагаемого определяется законом распределения и характеризует дифференциальную энтропию непрерывного источника (т. к. f(x) - плотность вероятности или дифференциальный закон распределения)

, (20)

Дифференциальная энтропия - часть энтропии источника непрерывных сообщений, которая зависит от плотности вероятности сигнала x(t) , выдаваемого источником.

Различные классы физических явлений и процессов подчиняются различным законам распределения. Непрерывные сигналы полностью характеризуются законами распределения (интегральным или дифференциальным). На любые реальные сигналы накладываются определенные ограничения, например: по средней мощности (нагрев аппаратуры); по мгновенной или пиковой мощности (перегрузки).

Так как дифференциальная энтропия зависит от плотности вероятности, определим, для какого закона она максимальна. Т. е. при каком распределении вероятности, сигнал заданной мощности имеет максимальную энтропию. Для нахождения максимального значения энтропии необходимо воспользоваться вариационной теоремой с использованием неопределенных множителей Лагранжа при условиях нормировки и неизменности среднего квадрата:

; .

При этом,

Решив уравнения, получим симметричный нормальный закон распределения

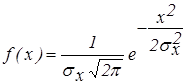. (11)

Если среднюю мощность не ограничивать

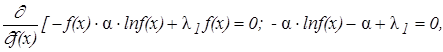
то получим равномерный закон распределения.

Определим дифференциальную энтропию для нормального распределения, т. е. сигнала с ограниченной средней мощностью. Полученное в результате решения вариационной задачи нормальное распределение является симметричным. Если в интеграле для дифференциальной энтропии произвести замену x = y-m_x ,то интеграл не изменится, а значит, энтропия не зависит от математического ожидания и равна энтропии центрированной случайной величины.

Определим максимальное значение для энтропии:

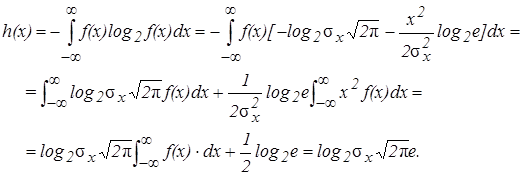
Дифференциальная энтропия для нормального распределения равна:

(12)

Полная энтропия для нормального распределения равна:

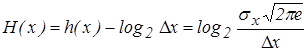. (13)