Контрольная работа: Финансовая математика 2

7000 + 12000x = 15 000.

Отсюда дробная часть срока окупаемости

x=7000/12000=0,58

Срок окупаемости равен 1 + x = 1,58.

Срок окупаемости с учетом времени по формуле:

v(i,1) R1+v(i,2) R2+…+v(i, [nok]) R [nok] +xv(i, [nok] +1) R [nok] +1=I0

приводит к уравнению

7000/1,1+12000/1,12x=15000; 7000*v(10%,1) +12000*v(10%,2) x=15000;

6363,64+9917,36x=15000; x=(15000-6363,64) /9917,36=0,87

Срок окупаемости с учетом времени поступления доходов равен 1,87.

Внутреннюю ставку дохода по определению находим из решения уравнения относительно i.

7000/(1+i) +12000/(1+i) 2=15000 или

15000х2-7000х-12000=0

где x = 1 + i. Сокращая на 1000, получим квадратное уравнение

15x2 - 7x - 12 = 0.

Положительный корень этого уравнения x1= 1,1577

Отсюда находим, что внутренняя ставка дохода

IRR = x1- 1 = 1,1577 - 1 =0,1577.

Вычисления по формулам проверим в Excel с помощью функций ЧПС и ВСД.

Исходные данные
ставка приведения	инвестиции	доходы
в конце 1 года	в конце 2 года
10%	-15 000,00р.	7000	12000
Решение
приведенные доходы	16 280,99р.
чистый приведенный доход	1 280,99р.
внутренняя ставка дохода	16%

Задание 4

На финансовом рынке может сложиться одна из четырех ситуаций A1, A2, A3, A4.

В условиях полной неопределенности инвестор выбирает из четырех финансовых операций F1, F2, F3, F4. Доходы инвестора определяются матрицей

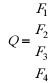
Определить оптимальный выбор финансовой операции по критериям Вальда и Сэвиджа.

1. Оптимальный выбор финансовой операции по критерию Вальда.

Найдем наихудший исход каждой финансовой операции, т.е. определим наименьшее число в каждой строке матрицы доходов:

a1= 14, a2= 8, a3= 11, a4= 12.

Согласно правилу Вальда, наибольшее среди найденных чисел определяет оптимальный доход. Следовательно, оптимальный доход равен 14, и он гарантируется выбором финансовой операции F1.

2. Оптимальный выбор финансовой операции по критерию Сэвиджа.