Контрольная работа: Фундаментальная группа. Конечные поля

Во всех случаях индекс внизу показывает число элементов групп.

На рисунке условно изображен двумерный клеточный комплекс, т.е. топологическое пространство, получающееся приклеиванием нескольких двумерных клеток (дисков) к одномерному комплексу (графу). Рисунок нужно понимать так: каждая «деталь» вида символизирует вершину графа, каждая склейка «отростков» вида

1. – ребро. Например, рисунок А символизирует граф на рисунке В.

Далее требуется получить копредставление фундаментальной группы, для этого проделаем следующее:

1) По очереди разрезаем рёбра графа, обозначая их буквами и указывая направления до тех пор, пока не получится дерево (связанный граф без циклов), см. рис. ниже. Эти буквы будут служить образующими группы:

2) Выписываем соотношения (слова), которые показывают, как кривые проходят по разрезанным рёбрам. Эти соотношения таковы: 1. 2. =1 3. =1 4. =1 5. =1 6. =1 3)Приводим выписанное копредставление к копредставлению одной из эталонных групп.

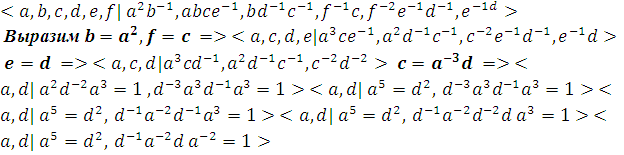Введём 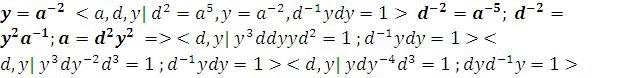В итоге получается , а именно