Контрольная работа: Геометрические свойства кривых второго порядка

Исследовать и изучить геометрические свойства кривых второго порядки (эллипса, гиперболы и параболы), представляющих собой линии пересечения кругового конуса с плоскостями, не проходящими через его вершины, а также научиться строить графики данных кривых в канонической и прямоугольной декартовой системах координат.

Постановка задачи

Дано уравнение кривой второго порядка:

. (1)

Задание . Для данного уравнения кривой второго порядка с параметром :

I . Определить зависимость типа кривой от параметра с помощью инвариантов.

II . Привести уравнение кривой при к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей.

III . Найти фокусы, директрисы, эксцентриситет и асимптоты (если они есть) данной кривой второго порядка.

IV . Получить уравнения канонических осей в общей системе координат.

V . Построить график кривой в канонической и общей системах координат.

Получение канонической системы координат. Построение графиков

I . Тип кривой второго порядка в зависимости от параметра

В прямоугольной декартовой системе координат кривая второго порядка задается в общем виде уравнением:

,

если хотя бы один из коэффициентов , , отличен от нуля.

Для уравнения кривой второго порядка (1) имеем:

Теперь определим тип данной нам кривой (1) с помощью инвариантов. Инварианты кривой второго порядка вычисляются по формулам:

;

;

.

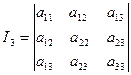Для данной кривой они равны:

1). Если , то уравнение кривой (1) определяет кривую параболического типа, но . Таким образом, если , то уравнение (1) определяет кривую параболического типа . При этом , то есть: если , то уравнение (1) определяет параболу .

2). Если, то данная кривая — центральная. Следовательно, при данная кривая — центральная .

· Если , то уравнение (1) определяет кривую эллиптического типа. Следовательно, если , то данная кривая есть кривая эллиптического типа . Но при этом . В соответствии с признаками кривых второго порядка получим: если, то уравнение (1) определяет эллипс .

· Если , то уравнение (1) определяет кривую гиперболического типа. Следовательно, если , то уравнение (1) определяет кривую гиперболического типа .

а) Если и , то уравнение (1) определяет две пересекающиеся прямые. Получим:

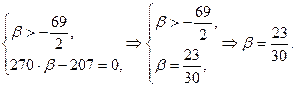
--> ЧИТАТЬ ПОЛНОСТЬЮ <--