Контрольная работа: Геометрические свойства кривых второго порядка

б) Если и , то данная кривая — гипербола. Но при всех за исключением точки . Следовательно, если , то уравнение (1) определяет гиперболу .

Используя полученные результаты, построим таблицу:

Значение параметра β
Тип кривой	Эллипс	Парабола	Гипербола	Две пересекающиеся прямые	Гипербола

II . Переход от общего уравнения кривой к каноническому

Рассмотрим теперь случай, когда, и исследуем данное уравнение кривой второго порядка с помощью инвариантов. Из вышеприведенной таблицы видим, что при уравнение (1) определяет гиперболу и принимает вид:

(2.1)

Приведем уравнение кривой (2.1) к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей.

Мы установили, что данная кривая — центральная, поэтому используем методику приведения к каноническому виду для уравнения центральной кривой. Совершим параллельный перенос начала координат в точку . При этом координаты произвольной точки плоскости в системе координат и координаты в новой системе координат связаны соотношениями

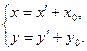
Подставляя эти выражения в уравнение (2.1), получим:

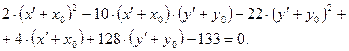(2.2)

Раскрывая скобки и приводя подобные члены, получим:

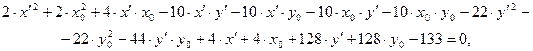
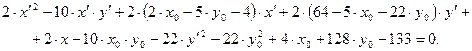(2.3)

В уравнении (2.3) коэффициенты при приравняем к нулю. Получим систему уравнений относительно

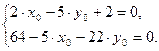(2.4)

Решив систему (2.4), получим:

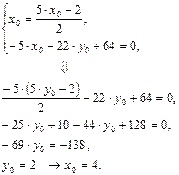
Центр кривой имеет координаты , . Поставим найденные значения в уравнение (2.3). В новой системе координат в уравнении (2.3) коэффициенты при равны нулю и уравнение примет вид

,

. (2.5)

Так как , то дальнейшее упрощение уравнения (2.5) мы достигаем при помощи поворота осей координат на угол . При повороте осей координат на угол координаты произвольной точки плоскости в системе координат и координаты в новой системе координат связаны соотношениями

(2.6)

Подставляя (2.6) в уравнение (2.5), получим

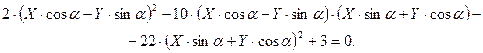
Раскроем скобки и приведем подобные члены

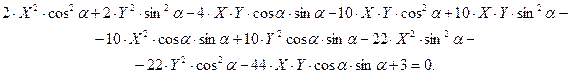
Приводя подобные члены, получим уравнение