Контрольная работа: Группировка коммерческих банков РФ по экономически чувствительным

сумма частот,

сумма накопленных частот, предшествующих медианному интервалу,

частота медианного интервала.

Рисунок 3.

2. Построим ряд распределения банков по возрасту.

Величина интервала:

Таблица 3.2

№	Группы банков по возрасту, лет	Число банков, Fi	Середина интервала, Xi	Xi*Fi	Сумма накопленных частот, S	Xi-X	(Xi-X)*Fi	(Xi-X)2	(Xi-X)2*Fi
1	5,0-5,8	12	5,4	64,8	12	1,25	15	1,56	18,72
2	5,8-6,6	5	6,2	31,0	17	0,45	2,25	0,2	1,0
3	6,6-7,4	3	7,0	28,0	20	0,35	1,4	0,12	0,48
4	7,4-8,2	2	7,8	15,6	22	1,15	2,3	1,32	2,64
5	8,2-9,0	7	8,6	60,2	29	1,95	13,65	3,8	26,6
ВСЕГО	29	-	199,6	-	-	34,6	-	49,44

Среднее значение показателя рассчитывается как средняя арифметическая интервального ряда по формуле:

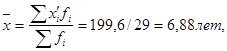
где середины интервалов;

частота го интервала.

Мода – значение признака, наиболее часто встречающееся в исследуемой совокупности, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.

Модальным интервалом является 1-ый интервал с частотой Fmo=12

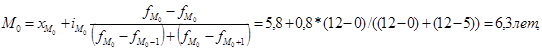
где нижняя граница модального интервала;

величина модального интервала,