Контрольная работа: Интеграл дифференциального уравнения

Контрольное задание:

Упражнения

1. Дана последовательность а_n =(3n-5)/(4n+1). Установить номер n₀ , начиная с которого выполняется неравенство │а_n -А │ < 1/500.

Отв. n₀ =719.

Найти:

2. lim (3-√х)/(х² -81).Отв. –1/108.

х→9

3. lim (5х² -8)/(х³ -3х² +11).Отв. 0.

х→∞

Проверить непрерывность следующих функций:

4. у=5х/(х³ +8).Отв. При всех х≠–2 функция непрерывна.

5. у=(х² +4)/ √(х² -36). Отв. Функция непрерывна при всех значениях

│х│>6.

6. Определить точки разрыва функции у=(8х+2)/(16х² -1).

Отв . Точки х₁ =–1/4 и х₂ =1/4.

Задача 1

Найти общий интеграл дифференциального уравнения:

Решение

Выполним разделение переменных, для этого разделим обе части уравнения на :

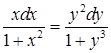
Проинтегрируем обе части уравнения и выполним преобразования:

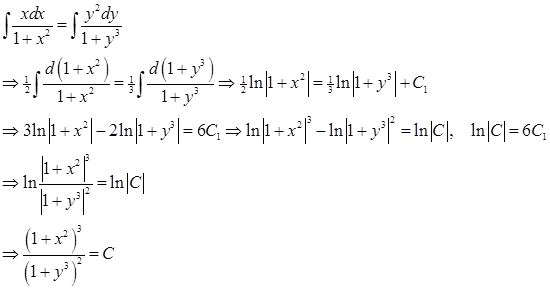
Ответ

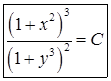
Задача 2

Проинтегрировать однородное дифференциальное уравнение:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--