Контрольная работа: Інженерні розрахунки в MathCad

Розв’язати систему нелінійних рівнянь:

sin (x) + sin (y) - 1.3 = 0

y² - x² +x = 0

с точністю e=0.00001.

Розв’язання:

Відомо, що розв’язком системи є такі значення х і у , які перетворюють одночасно обидва рівняння в тотожності.

Для знаходження розв’язку системи необхідно спочатку графічно знайти грубе наближення цих значень для х і у .

Очевидно, що потрібно побудувати криві, які описуються рівняннями системи. Координати точки перетину цих кривих (як спільна їх точка) і являтимуть розв’язком системи.

Щоб побудувати ці криві необхідно рівняння системи привести до виду:

y= f1 ( x)

y= f2 ( x),

тобто в нашому випадку:

.

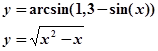Після цього побудувати графіки функцій:

.

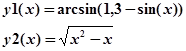Порядок дій:	Пояснення:
Описуємо дві функції користувача	Функції asin , sin і Öвибрати з панелі Calculator.
Будуємо графіки функцій: y1 (x) і y2 (x)
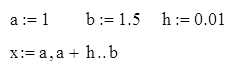	Довільно вибираємо відрізок [a,b], на якому будуємо графік функцій. Задаємо розбиття відрізку точками, описавши х як ранжовану змінну, яка змінюватиметься від а до b з кроком h . Якщо на вибраному відрізку [a,b] криві не перетнуться змінюмо до тих пір а і b поки не віднайдемо точку перетину.
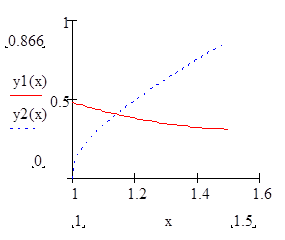	Із графіка приблизно знайти значення: х =1,2 і у = 0,4 координати точки перетинання графіків
Задаємо початкові значення розвязку: x: =1.2 y: = 0.4	Задаємо початкові значення для х і у .
	Задаємо точність обчислень
Уточнюємо розвязок до задоного ступеня точності. « 1 2 3 4 5 » К-во Просмотров: 234 Бесплатно скачать Контрольная работа: Інженерні розрахунки в MathCad >>> Скачать <<< Меню Поиск