Контрольная работа: Использование расчетных формул в задачах
Задача 1.
Определить центр тяжести сечения.
 |
Решение
Укажем оси координат X и Y с началом в нижнем левом углу сечения.
Сечение разобьем на два простых сечения – прямоугольник 1 с центром тяжести С1 и квадрат 2 с центром тяжести С2 .
Координаты центра тяжести С сечения находим по формулам:
и 
, где
x 1 = 15 мм - координата центра тяжести С1 прямоугольника по оси Х ;
y 1 = 30 мм - координата центра тяжести С1 прямоугольника по оси Y ;
x 2 = 45 мм - координата центра тяжести С2 квадрата по оси Х ;
y 2 = 15 мм - координата центра тяжести С2 квадрата по оси Y ;
F 1 = 
= 1800 мм2 - площадь прямоугольника;
F 2 = 
= 900 мм2 - площадь квадрата.
Тогда
мм, 
мм.
Задача 2.
К стальному валу приложены три известных момента М 1 , М 2 , М 3 . Требуется: 1) установить, при каком значении момента Х угол поворота правого концевого сечения вала равно нулю; 2) для найденного значения Х построить эпюру крутящих моментов; 3) при заданном значении [τ] определить диаметр вала из расчета на прочность и округлить его значение до ближайшего, равного 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм; 4) построить эпюру углов закручивания; 5) найти наибольший относительный угол закручивания (на 1 м).
Для стали принять G = 
МПа. Полярный момент инерции 
м4
a = 1,9 м, b = 1,2 м, c = 1,4 м,
М 1 = 1900 Нм, М 2 = 1200 Нм,
М 3 = 1700 Нм, [τ] = 75 МПа.
 |
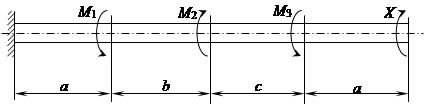Решение.
1) Угол поворота правого концевого сечения определяется как алгебраическая сумма взаимных углов поворота сечений на участках АВ, BC, CD, DE
.
Отсюда определим момент X
Х = 1178,125Нм
--> ЧИТАТЬ ПОЛНОСТЬЮ <--