Контрольная работа: Использование расчетных формул в задачах

при z = (a + b ) = 3,1 м = – 0,046 рад.

Участок BC :

, где

при z = (а + b ) = 3,1 м φ = – 0,046 рад;

при z = (a + b + c ) = 4,5 м = – 0,068 рад.

Участок AB :

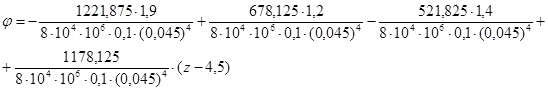, где

при z = (а + b + c ) = 4,5 м φ = – 0,068 рад;

при z = (2a + b + c ) = 6,4 м = 0 рад.

5) Наибольший относительный угол закручивания будет на участке DE

== 0,037 рад/м

Задача 3.

Для поперечного сечения, составленного из стандартных прокатных профилей, требуется:

1) определить положение центра тяжести;

2) найти значения осевых и центробежных моментов инерции относительно горизонтальной и вертикальной осей, проходящих через центр тяжести сечения;

3) определить направления главных центральных осей инерции;

4) найти значения моментов инерции относительно главных центральных осей;

5) вычертить сечение в масштабе 1:2 и указать на нем все оси и размеры.

Схема сечения состоит из двух прокатных профилей:

профиля I - швеллера № 30,

профиля II - двутавра № 33.

Решение.

Геометрические характеристики швеллера берем по ГОСТ 8240-72:

h^I = 300 мм, b^I = 100 мм, d^I = 6,5 мм, t^I = 11 мм,

см⁴ , см⁴ , А₁ = 40,5 см² , z ₀ = 2,52 см.

Геометрические характеристики двутавра берем по ГОСТ 8239-72:

h^II = 330 мм, b^II = 140 мм, d^II = 7 мм, t^II = 11,2 мм,

см⁴ , см⁴ , А₂ = 53,8 см² .

Выбираем вспомогательные оси V , Z и определяем относительно их координаты центра тяжести составного сечения