Контрольная работа: Исследование частотных характеристик типовых динамических звеньев

а) б)

а) ЛАЧХ и ЛФЧХ;

б) переходная функция

Рисунок 22 – Характеристики последовательно соединенных -цепочек с разделительным усилителем

При анализе частотных характеристик апериодических звеньев 2-го порядка можно сделать следующие выводы:

· увеличение (уменьшение) постоянной времени звена приводит к сдвигу ЛАЧХ и ЛФЧХ влево (вправо).

· увеличение (уменьшение) постоянной времени звена приводит к увеличению (уменьшению) времени переходного процесса.

· на полосу пропускания большее влияние оказывает большая постоянная времени

· при увеличении постоянной времени звена время переходного процесса увеличивается, а полоса пропускания уменьшается, следовательно, при увеличении времени переходного процесса полоса пропускания уменьшается и наоборот.

e. Аппроксимация апериодического звена 2-го порядка звеном 1-го порядка

Ввиду того, что апериодическое звено 2-го порядка можно аппроксимировать звеном 1-го порядка, если одна постоянная времени намного превышает вторую ( в 10 раз), сравним характеристики звена с постоянными времени и со звеном 1-го порядка, изображенным на рисунке 23.

Аппроксимация апериодического звена 2-го порядка звеном 1-го порядка

а) б)

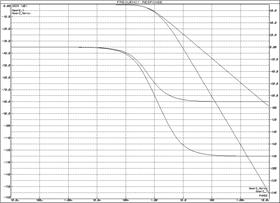
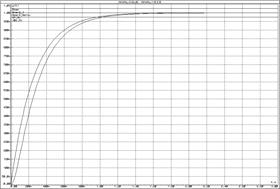
а) ЛАЧХ и ЛФЧХ;б) переходные функции

Рисунок 24 – Характеристики апериодического звена 2-го порядка и инерционного звена

При анализе характеристик апериодических звеньев (рисунок 24) можно сделать следующие выводы:

· апериодическое звено 2-го порядка можно аппроксимировать апериодическим звеном 1-го порядка, если первая постоянная времени намного меньше второй, т.к. в таком случае влияние первой экспоненты на форму выходного сигнала несущественно.

Исследование колебательного звена

При исследовании колебательного звена необходимо пронаблюдать за характером его частотных характеристикпри изменении постоянной времени и декремента затухания в пределах, указанных в индивидуальном задании. Т.е. необходимо исследовать частотные характеристики при постоянных времени и декременте затухания .

f. Исследование частотных характеристик колебательного звена при изменении постоянной времени () и неизменном декременте затухания ()

Для исследования колебательного звена при изменении постоянной времени () и неизменном декременте затухания в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 25. Логарифмические частотные характеристики колебательного звена представлены на рисунке 26, графики переходной функции – на рисунке 27.

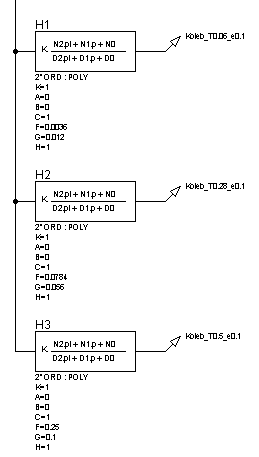
Рисунок 25 – Структурная схема для исследования колебательныхзвеньев при изменении постоянной времени () и неизменном декременте затухания ()

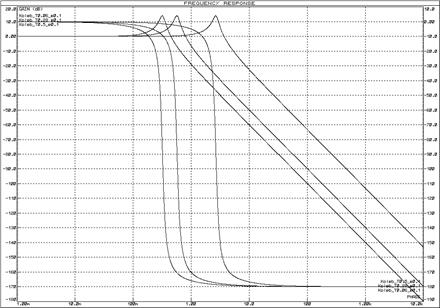
Рисунок 26 – Логарифмические частотные характеристики колебательных звеньев при изменении постоянной времени () и неизменном декременте затухания ()

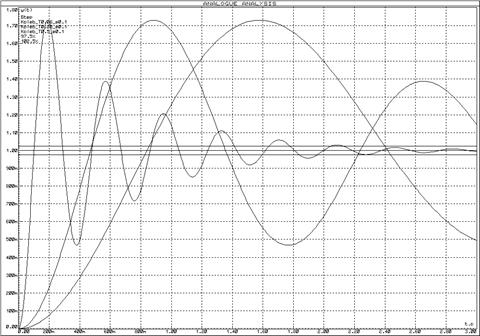
Рисунок 27 – Переходные функции колебательныхзвеньев при изменении постоянной времени () и неизменном декременте затухания ()

g. Исследование частотных характеристик колебательного звена при изменении постоянной времени () и неизменном коэффициенте демпфирования ()