Контрольная работа: Исследование частотных характеристик типовых динамических звеньев

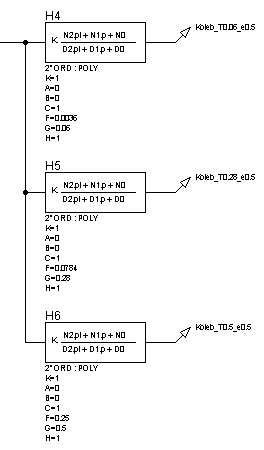
Рисунок 28 – Структурная схема для исследования колебательныхзвеньев при изменении постоянной времени () и неизменном декременте затухания ( )

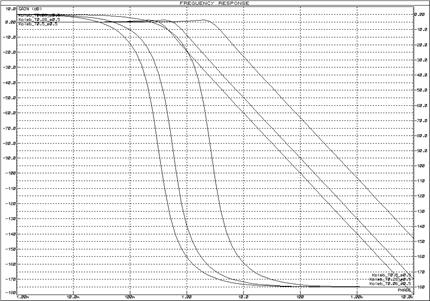
Рисунок 29 – Логарифмические частотные характеристики колебательных звеньев при изменении постоянной времени () и неизменном декременте затухания ( )

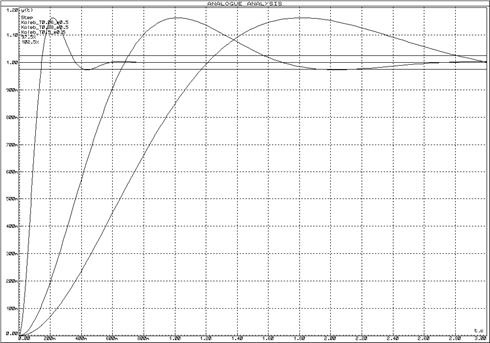
Рисунок 30 – Переходные функции колебательныхзвеньев при изменении постоянной времени () и неизменном декременте затухания ( )

h. Исследование частотных характеристик колебательного звена при неизмененной постоянной времени () и изменении декремента затухания ().

Для исследования колебательного звена при неизмененной постоянной времени () и изменении коэффициента демпфирования ( ) в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 31. Логарифмические частотные характеристики колебательного звена представлены на рисунке 32, графики переходной функции – на рисунке 33.

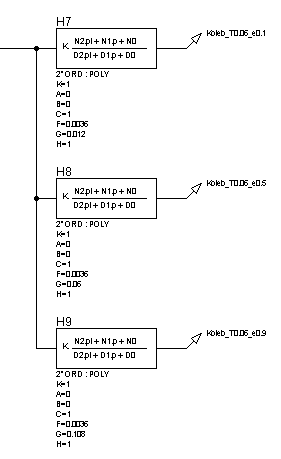
Рисунок 31 – Структурная схема для исследования колебательного звена при неизмененной постоянной времени () и изменении декремента затухания ()

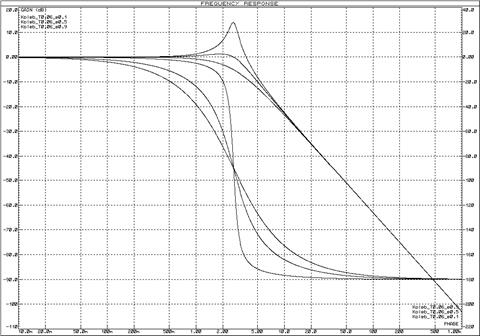
Рисунок 32 – Логарифмические частотные характеристики колебательных звеньев при изменении постоянной времени () и неизменном декременте затухания ()

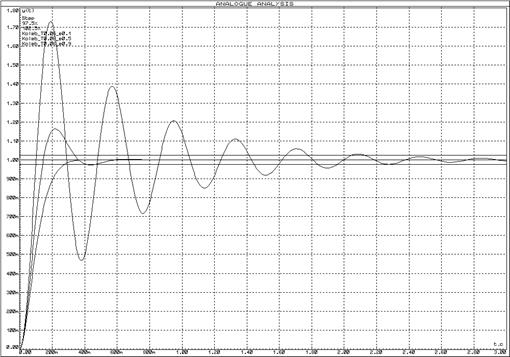
Рисунок 33 – Переходные функции колебательного звена при неизмененной постоянной времени () и изменении декремента затухания ()

i. Реализация колебательного звена

Реализуем колебательное звено с постоянной времени и коэффициентом демпфирования на -контуре (рисунок 34). ЛАЧХ и ЛФЧХ данного звена и необходимого колебательного звена представлены на рисунке 35, а, а их переходные функции – на рисунке 35, б.

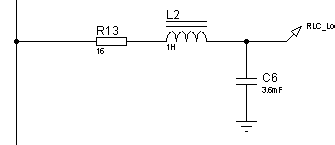
Рисунок 34 – Электрическая принципиальная схема колебательного -контура

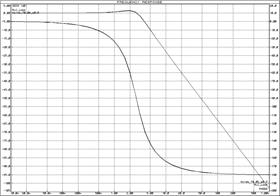
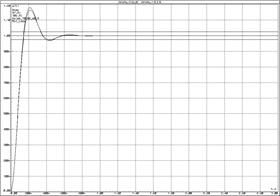
а) б)

а) ЛАЧХ и ЛФЧХ;б) переходная функция

Рисунок 35 – Характеристики колебательного звена и -контура

При анализе графиков частотных характеристик и переходных процессов (рисунок 35) колебательных звеньев можно сделать следующие выводы:

· увеличение (уменьшение) постоянной времени звена при неизменном декременте затухания приводит к сдвигу частотных характеристик влево (вправо).

· при неизменном коэффициенте демпфирования увеличение постоянной времени звена приводит к сужению полосы пропускания; колебательность переходного процесса не меняется.

· при неизменной постоянной времени увеличение (уменьшение) коэффициента демпфирования приводит к уменьшению (увеличению) колебательности переходного процесса и к более плавной ЛФЧХ.

· при неизменной постоянной времени увеличение (уменьшение) коэффициента демпфирования приводит к уменьшению (увеличению) перерегулирования, сужению (расширению) полосы пропускания и уменьшению (увеличению) колебательности.

3. Исследование дифференцирующих звеньев

a. Исследование частотных характеристик идеального дифференцирующего звена