Контрольная работа: Исследование экономико-математических моделей
Оценить эффективность и масштаб производства.
На основе построенной регрессии развязать задачу оптимального выпуска продукции: определить, какая комбинация факторов производства является оптимальной, а также найти максимальный объем выпуска, если на расходы производства существует ограничение в 160 тыс. грн., стоимость аренды единицы фондов составляет (4+K) тыс. грн., стоимость труда одного человека – (1+K) тыс. грн.
Построить изокванту максимального выпуска и изокосту. Найти графическое решение задачи о комбинации ресурсов и сравнить с аналитическим.
Определить предельную норму замены единицы фондов трудом.
Производственная фирма выпускает продукцию согласно варианта 14 с применением труда рабочих и основных средств производства (табл. 2.1).
Таблица 2.1
|
В |
Х1 |
Х2 |
| 292 | 64 | 91 |
| 312 | 74 | 101 |
| 332 | 84 | 111 |
| 353 | 94 | 121 |
| 372 | 104 | 131 |
| 393 | 114 | 141 |
| 415 | 124 | 151 |
| 433 | 134 | 161 |
| 454 | 144 | 171 |
| 474 | 154 | 181 |
| 494 | 164 | 191 |
Найдем точечные оценки параметров множественной линейной регрессии с помощью функции Excel ЛИНЕЙН.
Но согласно этого задания связь в модели полный функциональный R2 = 1, R = 1, коэффициенты детерминации и корреляции равняются 1 (также и в модели множественной линейной регрессии) – нет смысла бедствовать множественную линейную регрессию (рис. 2.1)

Рис. 2.1.
Задание №3 (оценивается в 10 баллов)
Значения объемов производства некоторой фирмы и соответствующих расходов производства приведены в таблице:
| Объем производства Y | Расходы производства C | Цена p. |
| 20+N/5 | 190+N-K | 16 |
| 30+N/5 | 210+N-K | 16 |
| 25+N/5 | 100+N-K | 14 |
| 35+N/5 | 230+N-K | 14 |
| 40+N/5 | 240+N-K | 13 |
| 50+N/5 | 400+N-K | 12 |
| 60+N/5 | 375+N-K | 15 |
| 55+N/5 | 330+N-K | 12 |
| 55+N/5 | 280+N-K | 12 |
| 70+N/5 | 470+N-K | 13 |
| 65+N/5 | 400+N-K | 13 |
| 75+N/5 | 550+N-K | 12 |
| 70+N/5 | 600+N-K | 12 |
Построить квадратичную зависимость расходов производства от объемов производства и оценить статистическое качество модели, что построено.
1. Для условий совершенной рыночной конкуренции (если значение цены на продукцию фирмы) необходимо сделать следующее:
Построить функции маржинальных расходов и дохода и построить их графику. Графически определить оптимальный объем производства.
Аналитически определить оптимальный объем производства фирмы, за которого прибыль фирмы будет максимальной, и определить соответствующий данному объему производства прибыль. Определить объем производства, за которого прибыль фирмы будет неотъемлемой.
2. Для условий монополии фирмы на рынке (значение цены на продукцию фирмы для этого случая приведено в таблице) необходимо сделать следующее:
Построить линейную зависимость цены от объемов производства и оценить статистическое качество модели, что построено.
Построить функции маржинальных расходов и дохода и построить их графику. Графически определить оптимальный объем производства.
Аналитически определить оптимальный объем производства фирмы, за которого прибыль фирмы будет максимальной, и определить соответствующий данному объему производства прибыль. Определить объем производства, за которого прибыль фирмы будет неотъемлемой.
Проанализировать и описать полученные результаты.
Расчетная таблица для варианта 14 выглядит следующим образом:
| Объем производства Y | Расходы производства C | Цена, р |
| 22,8 | 203 | 16 |
| 32,8 | 223 | 16 |
| 27,8 | 113 | 14 |
| 37,8 | 243 | 14 |
| 42,8 | 253 | 13 |
| 52,8 | 413 | 12 |
| 62,8 | 388 | 15 |
| 57,8 | 343 | 12 |
| 57,8 | 293 | 12 |
| 72,8 | 483 | 13 |
| 67,8 | 413 | 13 |
| 77,8 | 563 | 12 |
| 72,8 | 613 | 12 |
Корреляционное поле с линией квадратичного тренда (рис. 3.1):
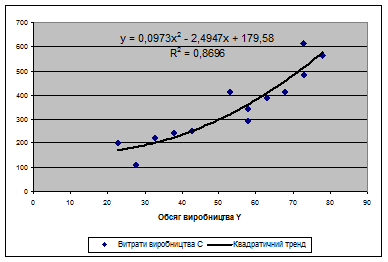
Рис. 3.1.
Уравнение квадратичного тренда: в = 0,0973х2 – 2,4947х + 179,58.