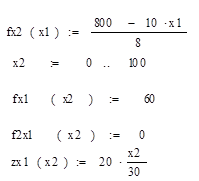Контрольная работа: Исследование операций математической модели
С точки зрения математики производственную программу предприятия в первом приближении можно записать как набор чисел х1,х2,…,хn котором хi обозначает запланированный выпуск изделий i-го типа, n — количество типов изделий.
Если Ci — доход от произведенного изделия i-го типа и каждое произведенное изделие покупается по одной и той же цене, то суммарный доход предприятия является простой суммой]
х1 – запланированный выпуск радиоприёмников первой модели
х2 – запланированный выпуск радиоприёмников второй модели
Другим неотьемлимым элементом экономической ситуации являются ограничения, налагаемые на возможные варианты планов производства.
Чаще всего это так называемые ресурсные ограничения, описывающие тот факт, что для производства товаров приходиться тратить ресурсы;
количество ресурсов, которое можно затратить на производство
товаров, ограничено.
Если считать, что в нашем производстве используются ресурсы i=1,2,…,n, то в модели линейного программирования эти два факта описываются с помощью коэффициентов aij, которые задают затраты i-го ресурса на производство единицы j –го продукта.
Если затраты ресурсов линейно возрастают в зависимости от роста объемов производства, то для выпуска продукта j в количестве xj единиц aijxj i-го ресурса. Выпуск всего плана x = (Х1,Х2,... ,хn) потребует при этом
![]()
единиц i-го ресурса.
Когда в наличии имеется не более bi единиц этого ресурса, то ясно, что любой реализуемый план производства x должен удовлетворять ограничению
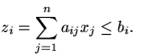
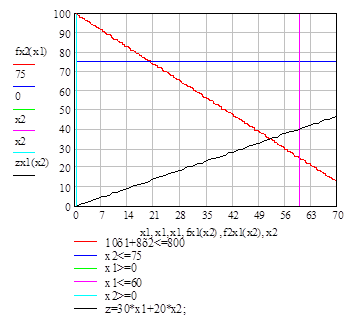
Ограничения по условию задачи:
1) 10х1 + 8х2 ≤ 800
2) х1 ≤ 60
3) х2 ≤ 75
4) х1 >=0
5) х2 >=0
Целевая функция:
z =30х1 + 20х2
В приведенном выше примере естественным экономическим требованием является максимизация дохода предприятия, что будет записываться как
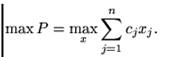
Максимум дохода достигается за счет оптимального выбора производственной программы.
Из этих условий строим графически область допустимых решений (ОДР).