Контрольная работа: Исследование операций математической модели

Х1 = 60 изделий.

Х2 = (800 – 10*60)/8 = 25 изделий.

Общая прибыль составляет

Р = 60*30 + 25*20 = 2300 у.е.

Исследование модели на чувствительность

Цель анализа чувствительности - оценить предельное возрастание дефицитного ресурса, ведущее к росту прибыли.

Если задача разрешима, то, кроме данного случая единственного решения, задача может иметь бесконечное множество решений - альтернативный оптимум. В этом случае прямая, соответствующая целевой функции, параллельна прямой, соответствующей одному из связывающих ограничений. Ограничение называют связывающим, если прямая, его представляющая, проходит через оптимальную точку.

Поскольку решение связано с точкой Q, то произведем исследование на чувствительность по прямым, пересекающихся в точке Q.

Сдвигая в сторону точки W, второй модели радиоприёмников будет уменьшаться, а количество радиоприёмников первой модели останется на том же уровне.

Рw = 60*30 + 0*20 = 1800 у.е.

Что на 500 у.е. меньше оптимального.

При дальнейшем исследовании модели на чувствительность начнём её перемещение по отрезку QR в сторону увеличения числа радиоприёмников второго типа и уменьшения числа первого.

Рe = 56*30 + 30*20 = 2280 у.е.

Что меньше оптимума на 20 у.е..

При дальнейшем продвижении по отрезку мы придём в точку R. В точку с максимально большим количеством радиоприёмников 1-й модели.

Рr = 20*30+75*20 = 2100 у.е.

Что на 100 у.е. меньше оптимального.

При устранении ограничения Х2=75, мы придём к точке E2 на прямой 0Х2 , в которой прибыль будет равна Р = 100*20=2000, что на 300 у.е. меньше найденного оптимального в т.Q

При устранении ограничения Х1=60, мы придём к точке W2 на прямой 0Х1, в которой выпуск радиоприёмников второй модели равен нулю, а прибыль от производства будет:

Р = 80*30=2400, что на 100 у.е. больше оптимального в т.Q

Самое большое ограничение накладывается на максимальном запасе деталей:

Х1=60 и Х2=75.

Р=60*30+75*20=3300 у.е.

Т.е. при устранении мы приобретаем дополнительную прибыль – 1000 у.е.

На решение задачи имеют влияния ресурсы, а точнее их значение. Ресурсы можно разделить на дефицитные, которые при любом, даже незначительном уменьшении, влияют на решение задачи, и недефицитные, которые при уменьшении не влияют на решение задачи, пока они не переходят в категорию дефицитных (ОДР)

В данной задаче имеются 2 ресурса, охаратеризованные в уравнениях (1) и (2), оба они являются дефицитными, то есть их изменение приводит к перемещению точки оптимального решения.

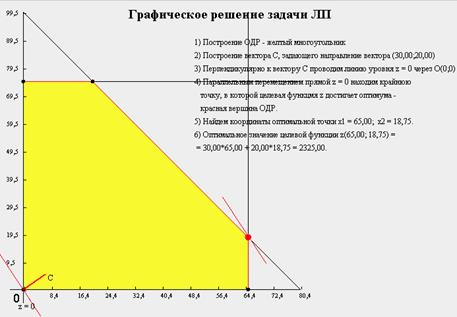
1)Рассмотрим 2 ограничение:

Увеличим его количество до 65