Контрольная работа: Исследование зависимости между объемом производства, капитальными вложениями и выполнением норм

или

Итак, с вероятностью 0,52 можно утверждать, что неизвестное знамение параметра регрессии содержится в интервале

При построении доверительного интервала для коэффициента корреляции генеральной совокупности прибегают к преобразованию Фишера по формуле (3.46):

Подставляя выборочный коэффициент корреляции получаем значение :

Стандартную ошибку вычисляем по приближенной формуле (3.47):

0,333.

Доверительные границы для величины на заданном уровне значимости определяются по формуле (3.48): .

При уровне значимости . Таким образом, доверительные границы для величины при будут следующими:

или

и доверительный интервал для

Доверительные границы для коэффициента корреляции находят путем обратного пересчета величины по формуле (3.49):

=

Итак, с вероятностью 0,5% можно утверждать, что коэффициент корреляции в генеральной совокупности содержится в интервале

Г) Построим уравнение регрессии и выполнить исследование множественной модели в полном объеме (см.п.3.2).

Будем искать зависимость объёма производства, капиталовложениями и выполнением норм выработки в виде линейной множественной регрессии.

(3.55)

Объясняющие переменные Х₁ и Х₂ оказывают совместное одновременное влияние на зависимую переменную У.

Приведем формулы для вычисления по МНК

(3.56)

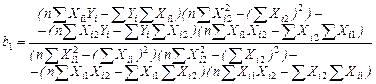(3.57)