Контрольная работа: Конструирование узлов и деталей машин

Δl =

=

= 0,000353 м = 0,353 мм.

Задача №2

Найти угол наклона сечения, для которого нормальное и касательное напряжения равны по абсолютной величине. Тело испытывает линейное напряженное состояние.

Решение.

Так как тело испытывает линейное напряженное состояние, то лишь одно из главных напряжений не равно нулю.

Рассмотрим наклонное сечение (рис. 2) под углом α. В рассматриваемом сечении действует напряжение р_а , направленное вдоль оси.

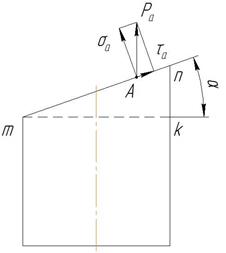
Разложим напряжение р_а на составляющие: касательные напряжения τ_а , лежащие в плоскости mn и нормальные σ_а , перпендикулярные плоскости mn. Тогда:

σ_а = р_а ∙ cos α,

τ_а = р_а ∙ sin α.

Из предыдущих соотношений видно, что σ_а = τ_а при α = 45°, cos 45° = sin 45°.

Задача №3

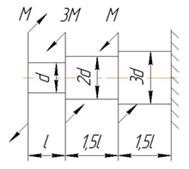
Построить эпюры М_кр , φ и определить τ_max для заданного вала с поперечным моментом сечения W_p для следующей схемы нагружения.

Решение.

Заданный вал имеет три участка нагружения (рис. 3). Возьмем произвольное сечение в пределах участка 1 и отбрасываем правую часть бруса. На оставленную часть бруса действуют моменты М и М_z ^I . Следовательно:

М_z ^I = -М.

Рассмотрим участок 2:

М_z ^II = 3M – M = 2M.

Рассмотрим участок 3:

М_z ^III = 3M + M – M = 3M.

Полярный момент сопротивления поперечного сечения для круга:

W_p = πd³ /16.

Вычисляем максимальные касательные напряжения в поперечных сечениях каждого участка.

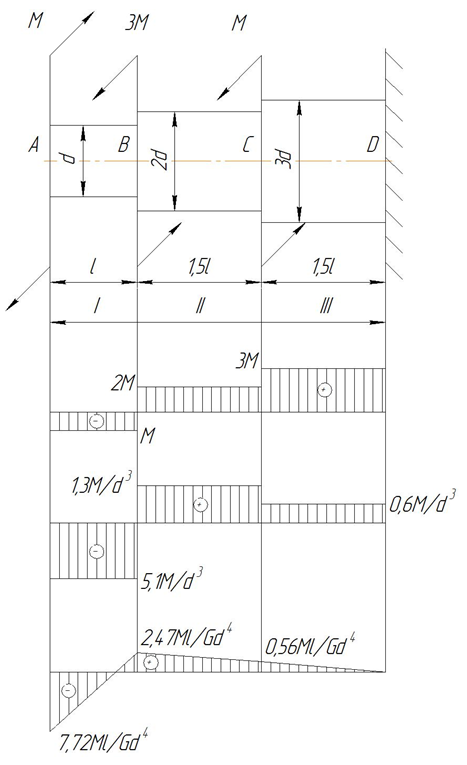
Знак касательных напряжений обусловлен знаком крутящего момента: