Контрольная работа: Кривые второго порядка. Квадратичные формы

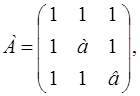М₁ = 1 > 0,

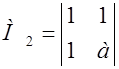= а – 1 > 0 Þ а > 1.

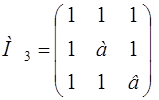= ав – а – в > 0 Þв > .

Ответ:

а > 1, в > .

Пример 4.

При каких значениях а и в квадратичная форма будет отрицательно определенной?

j (х₁ , х₂ , x₃ ) =

Решение.

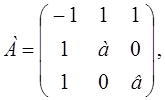М₁ = –1 < 0,

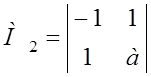= –а – 1 > 0 Þ а < –1.

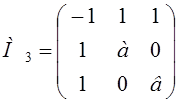= –ав – а – в < 0 Þв > – .

Ответ

а < –1, в > –.

Пример 5.

Доказать, что квадратичная форма

j (х₁ , х₂ , x₃ ) =

положительно определена.

Решение.

Воспользуемся критерием Сильвестра. Построим матрицу А и найдем главные миноры матрицы А.

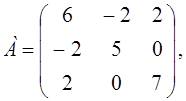
М₁ = 6 > 0, 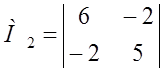= 26 > 0, М₃ = ú А ç = 162 > 0

Þj (х₁ , х₂ , x₃ )

положительно определенная квадратичная форма.

Литература

1. Гусак А. А. Аналитическая геометрия и линейная алгебра.– Мн.: Тетрасистемс, 1998.

2. Овсеец М. И., Светлая Е. М. Сборник задач по высшей математике. Учебное издание.– Мн.: ЧИУиП, 2006.– 67 с.