Контрольная работа: Математическая логика

Пример.

Пусть п = 4, k = 2. Тогда разложение Шеннона будет иметь вид

Следствие.

Предельное разложение Шеннона (k = n ) булевой функции имеет вид

.

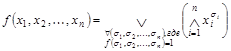Предельное разложение Шеннона булевой функции является ее СДНФ.

В алгебре логики справедлив принцип двойственности. Согласно этому принципу, будем иметь следующие двойственные разложения Шеннона булевой функции :

по k переменным

двойственное предельное разложение

.

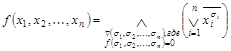Двойственное предельное разложение Шеннона булевой функции является ее СКНФ.

2 Булевы функции двух переменных

Рассмотрим простой бинарный элемент – выключатель, который имеет два состояния. Если данный выключатель контролируется входной переменной х ,то говорят, что он выключен (открыт) при х = 0 и включен (закрыт) при х = 1, как показано на рис. 1:

х = 0 х = 1

Рис. 1 - Два состояния выключателя

Будем использовать следующее графическое обозначение для представления таких выключателей:

х

Рис. 2 - Графическое обозначение выключателя

Рассмотрим соединения лампы с источником питания, представленные следующими схемами:

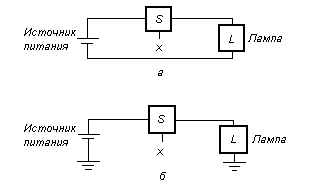
Рис. 3 - Лампа, управляемая выключателем: а – простое соединение с батареей; б – использование заземления, как обратной связи

Используя условное обозначение L , можно описать состояние лампы как функции входной переменной. Если лампа светится, то L = 1. Если лампа не светится, то L = 0. Поскольку L = 1 при х = 1, L = 0 при х = 0, то можно говорить, что L (х ) = х – логическая функция, х – логическая переменная. Это простое логическое выражение описывает выход как функцию от входа.

2.1 Булевы функции от двух переменных