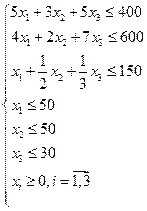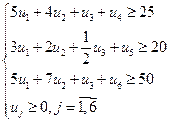Контрольная работа: Математический расчет объема выпуска продукции
![]()
![]()
3) x9
b6=30
![]()
![]()
![]()
1) От итоговой симплекс-таблицы прямой задачи перейдем к решению двойственной.
Сформулируем двойственную задачу:
- Так как прямая задача- задача на максимум, то двойственная ей задача на минимум.
- Коэффициенты функции цели прямой задачи будут коэффициентами вектора ограничений для двойственной.
- Коэффициенты вектора ограничений прямой задачи будут коэффициентами функции цели для двойственной.
- Ограничения двойственной задачи будут иметь знак ≥
| Прямая задача |
|
|
| Двойственная задача |
|
|
Для удобства перехода между прямой и двойственной задачами подпишем внутри последней симплекс-таблицы соответствующие переменные двойственной задачи
| БП | U7 | U8 | U9 | U1 | U2 | U3 | U4 | U5 | U6 | |||
| Двойств | Вi | A1 | А2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | ||
| 1 | A1 | U7 | 20 | 1 | 0 | 0 | 0,2 | 0 | 0 | 0 | -0,6 | -1 |
| 2 | A5 | U2 | 210 | 0 | 0 | 0 | -0,8 | 1 | 0 | 0 | 0.4 | -3 |
| 3 | A6 | U3 | 95 | 0 | 0 | 0 | -0,2 | 0 | 1 | 0 | 0,1 | 2/3 |
| 4 | A7 | U4 | 30 | 0 | 0 | 0 | -0,2 | 0 | 0 | 1 | 0.6 | 1 |
| 5 | A2 | U8 | 50 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 6 | A3 | U9 | 30 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| ∆j=W(j)-cj | 3000 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 5 | 25 | ||
Итоговая симплекс-таблица двойственной задачи:
| БП | Сбаз | Вi | C1=400 | С2=600 | C3=150 | C4=50 | C5=50 | C6=30 | C7=0 | C8=0 | C9=0 | |
| U1 | U2 | U3 | U4 | U5 | U6 | U7 | U8 | U9 | ||||
| 1 | U1 | 400 | 5 | 1 | 0.8 | 0.2 | 0.2 | 0 | 0 | -0.2 | 0 | 0 |
| 2 | U5 | 50 | 5 | 0 | -0.4 | -0.1 | -0.6 | 1 | 0 | 0.6 | -1 | 0 |
| 3 | U6 | 30 | 25 | 0 | 3 | -2/3 | -1 | 0 | 1 | 1 | 0 | -1 |
| ∆j=Z(j)-cj | 0 | -210 | -95 | 30 | 0 | 0 | -20 | -50 | -30 | |||
Оптимальным решением двойственной задачи будет:
| Свободные переменные | Базисные переменные |
|
U2=0 U3=0 U4=0 U7=0 U8=0 U9=0 |
U1=5 К-во Просмотров: 588
Бесплатно скачать Контрольная работа: Математический расчет объема выпуска продукции
|