Контрольная работа: Математический расчет объема выпуска продукции

Так как в строке №1 нет ни одного отрицательного коэффициента то решения НЕТ!

Возможно в условии задачи вместо МИНИМАЛЬНОГО спроса имели ввиду МАКСИМАЛЬНЫЙ.

Решим задачу для условия, что максимальный спрос на изделия составляет 50, 50 и 30единиц.

Тогда математическая модель задачи:

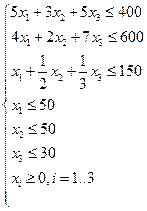
Канонический вид задачи линейного программирования:

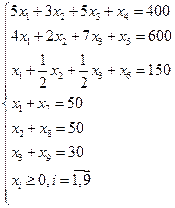
х1, х2, х3- свободные переменные

х4, х5, х6, х7, х8, х9- базисные переменные

Составим и заполним 1-ую симплексную таблицу для нового условия задачи:

БП	C1=25	С2=20	C3=50	C4=0	C5=0	C6=0	C7=0	C8=0	C9=0
	Сб	Вi	A1	А2	A3	A4	A5	A6	A7	A8	A9
1	A4	0	400	5	3	5	1	0	0	0	0	0
2	A5	0	600	4	2	7	0	1	0	0	0	0
3	A6	0	150	1	1/2	1/3	0	0	1	0	0	0
4	A7	0	50	1	0	0	0	0	0	1	0	0
5	A8	0	50	0	1	0	0	0	0	0	1	0
6	A9	0	30	0	0	1	0	0	0	0	0	1
∆j=W(j)-cj			0	-25	-20	-50	0	0	0	0	0	0

Находим пробное решение, для этого все свободные переменные приравниваем к 0, а базисные к bi

Свободные переменные	Базисные переменные
X1=0 X2=0 X3=0	X4=400 X5=600 X6=150 X7=50 X8=50 X9=30

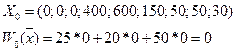
Решение ОПОРНОЕ, так как все коэффициенты в столбце bi>=0.

Для того что бы задача МАКСИМУМ имела оптимальное решение, необходимо, что б все коэффициенты в строке функции цели ∆j=W(j)-cj были не отрицательные (∆j≥0). У нас в этой строке есть отрицательные коэффициенты, поэтому решение НЕ ОПТИМАЛЬНОЕ.

Всего у нас три столбца у которых оценка плана отрицательна А1, А2 и А3.

Рассмотрим каждый из них и выберем тот который более выгодно ввести в базис. (Другими слова, при вводе какого вектора функция цели будет иметь наибольшее изменение)

А1 столбец:

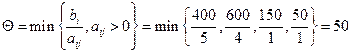
Функция цели меняется по формуле: