Контрольная работа: Математический расчет объема выпуска продукции

X2=0

X4=0

X9=0

X1=50

X3=30

X5=190

X6=90

X7=0

X8=50

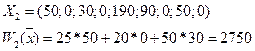
Решение опорное, но не оптимальное.

Разрешающий столбец № 2 (вектор А2 так как только у него есть отрицательная оценка плана)

Найдем разрешающий столбец:

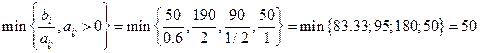
БП	C1=25	С2=20	C3=50	C4=0	C5=0	C6=0	C7=0	C8=0	C9=0
	Сб	Вi	A1	А2	A3	A4	A5	A6	A7	A8	A9
1	A1	25	20	1	0	0	0,2	0	0	0	-0,6	-1
2	A5	0	210	0	0	0	-0,8	1	0	0	0.4	-3
3	A6	0	95	0	0	0	-0,2	0	1	0	0,1	2/3
4	A7	0	30	0	0	0	-0,2	0	0	1	0.6	1
5	A2	20	50	0	1	0	0	0	0	0	1	0
6	A3	50	30	0	0	1	0	0	0	0	0	1
∆j=W(j)-cj			3000	0	0	0	5	0	0	0	5	25

соответствует строке №5 и вектору А8

Меняем А8—А5

Находим пробное решение, для этого все свободные переменные приравниваем к 0, а базисные к bi

Свободные переменные	Базисные переменные
X4=0 X8=0 X9=0	X1=20 X2=50 X3=30 X5=210 X6=95 X7=30

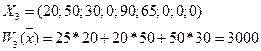
Решение ОПОРНОЕ и ОПТИМАЛЬНОЕ! Все коэффициенты в строке ∆j≥0

Для получения максимальной прибыли необходимо выпускать товар в следующем ассортименте: