Контрольная работа: Математический расчет объема выпуска продукции

Задача №11

G=5

N=25

Завод выпускает изделия трех моделей (1, 2 и 3). Для изготовления используются 2 вида ресурсов А и В, запасы которых составляют 400 и 600 единиц. Расход ресурсов на одно изделие каждой модели приведен в таблице:

Расход ресурса на одно изделие
Изделие 1	Изделие 2	Изделие 3
Ресурс А	G=5	3	5
Ресурс В	4	2	7

Трудоемкость изготовления изделия 1 вдвое больше, чем изделия модели 2 и в трое больше, чем модели 3. Численность рабочих завода позволяет выпускать 150 изделий модели 1 (если не одновременно изделия моделей 2 и 3). Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 50, 50 и 30 изделий моделей 1, 2 и 3 соответственно. Удельные прибыли от реализации изделий 1, 2 и 3 составляют N=25 , 20 и 50$ соответственно.

Определить объемы выпуска изделий каждой модели, при которых прибыль будет максимальна.

Необходимо:

1) Составить математическую модель задачи целочисленного программирования.

2) Решить задачу симплекс-методом.

3) Произвести постоптимальный анализ.

4) Сформулировать двойственную задачу и от финального решения прямой задач перейти к решению двойственной задачи.

5) Найти целочисленное решение методом отсечения (достаточно пяти итераций).

1) Составим математическую модель задачи целочисленного программирования

Пусть х1 -выпущенное количество изделий модели 1

х2- выпущенное количество изделий модели 2

х3- выпущенное количество изделий модели 3

Хотим найти такой ассортимент выпускаемых товаров, при котором прибыль будет максимальнаПрибыль от продаж 1 единицы каждого изделия 25, 20 и 50$Записываем функцию цели:

Сырье которое используем в ходе производства ограничено запасами, построим ограничения по сырью, используя данные приведенные в таблице:

Численность рабочих позволяет выпускать только 150 единиц товара №1 если не производить в это же время товары 2 и 3.

Трудоемкость товара 1 вдвое больше чем товара 2 и втрое больше чем товара 3

По условию задачи сказано, что минимальный спрос на продукцию завода составляет 50, 50 и 30 изделий моделей 1, 2 и 3 соответственно:

Запишем все в математическую модель задачи:

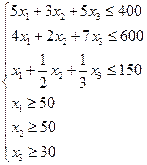
--> ЧИТАТЬ ПОЛНОСТЬЮ <--