Контрольная работа: Математическое моделирование в управлении
– установить курсор на ячейке, содержащей значение функции Q (Q2 ) ;
– Сервис – Поиск решения ;
– в появившемся диалоговом окне Поиск решения (рис.11) проверить, стоит ли в поле Установить целевую ячейку адрес функции Q (Q2 ), и если нет, то ввести его;
– в поле Равной щелкнуть пункт минимальному значению ;
– в поле Изменяя ячейки ввести диапазон ячеек, которые отведены для значений искомых параметров 
;
– щелкнуть по кнопке Выполнить;
– если решение найдено, сообщение об этом появится в диалоговом окне, где нужно щелкнуть по пункту Сохранить найденное решение. Значения 
найдены и находятся в отведенных для них ячейках (рис.10).
– Значение суммы квадратов отклонений найденной оценки функции регрессии от наблюденных значений результирующего признака , т.е. функции Q для линейной регрессии и функции Q2 для квадратичной регрессии , находятся в ячейках F53 и I53, линейная величина отклонений – в ячейке F54 и в ячейке I54.
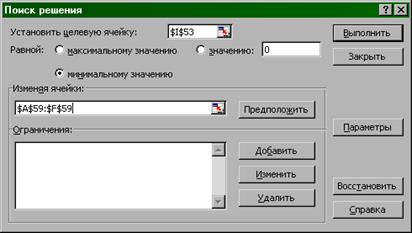
Рис.11. Ввод информации для Поиска решения.
Таким образом, коэффициенты линейной функции регрессии P(x) следует считывать из ячеек A56,B56 и С56; коэффициенты нелинейной функции регрессии P2 (x) – из ячеек A59 
F59. Для рассматриваемого примера линейная функция регрессии совпадает с полученной с помощью инструмента Регрессия , а квадратичная
P 2 ( x ) = 247,9641 – 930,3571 x 4 + 73,538 x 8 + 1009,39 x 4 2 – 4,44689 x 8 2 – 140,1884 x 4 x 8
Проверка значимости полученной квадратичной оценки уравнения регрессии выполним так. Определим коэффициент корреляции значений эмпирической функции регрессии и выборочного среднего RyP2 (x). Как видно из рис.12 , коэффициент корреляции достаточно большой (0,80921). Выполним еще одну проверку значимости P2 (x) с помощью коэффициента детерминации, для чего необходимо вычислить значения Sост , Sфакт .
Размещение нужных формул приведено на рис.12, а промежуточные результаты и значения коэффициента детерминации ниже. Поскольку коэффициент детерминации для случая квадратичной регрессии значительно превосходит коэффициент детерминации для случая линейной регрессии и имеет достаточно большое значение (0,472867), делаем вывод, что квадратичная регрессия достаточно хорошо согласуется со статистическими данными.
Выполним оценку значимости полученного приближения функции в целом с помощью критерия Фишера. Для этого найдем значения критерия Фишера по выборке для рассматриваемых двух видов зависимости (см. рис.12 и 13).
|
R |
S | |||
|
1 |
RyP(x) |
RyP2 (x) | ||
|
2 |
=КОРРЕЛ(C2:C52;D2:D52) |
=КОРРЕЛ(C2:C52;H2:H52) | ||
|
3 |
|
| ||
|
4 | ||||
|
5 |
=F53/48 |
К-во Просмотров: 504
Бесплатно скачать Контрольная работа: Математическое моделирование в управлении
|