Контрольная работа: Математичні моделі задач лінійного програмування
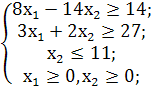
![]()
Розв’язок
Пряма задача лінійного програмування має вигляд:
![]()
При обмеженнях:
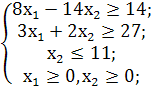
Оскільки, у прямій задачі лінійного програмування необхідно знайти мінімум функції, то приведемо першопочаткову умову до вигляду:
![]()
Для досягнення відповідного вигляду помножимо 3-ю нерівність на -1
0х1-11х2≥-11
В результаті отримаємо наступні матриці:
![]()
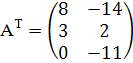
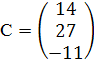
Для складання двоїстої задачі лінійного програмування знайдемо матриці А, В, СТ.
![]()
![]()
![]()
Відповідно, двоїста задача лінійного програмування матиме вигляд:
F(Y)= 14Y1+27Y2-11Y3 (max)
Обмеження:
8Y1+3Y2+0Y3≤5
-14Y1+2Y2-11Y3≤3
Y1≥0
Y2≥0
Y3≥0
Розв’яжемо задачу лінійного програмування симплексним методом.
Визначимо мінімальне значення цільової функції F(X) = 5x1+3x2 при наступних умовах-обмежень.