Контрольная работа: Математичні моделі задач лінійного програмування

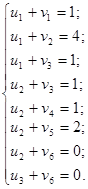
Записана система рівнянь є невизначеною, і один з її розв’язків дістанемо, узявши, наприклад, u1 = 0. Тоді всі інші потенціали однозначно визначаються з цієї системи рівнянь: u1 =0, u2 = 0, u3 = 0, v1 =1, v2 =4, v3 =1 v4=1, v5=2, v6=0. Ці значення потенціалів першого опорного плану записуємо у транспортну таблицю.

Потім згідно з алгоритмом методу потенціалів перевіряємо виконання другої умови оптимальності ui + vj ≤ cij(для порожніх клітинок таблиці):

А1B4 : u1 + v4 = 0 + 1 = 1<5;

А1B5 : u1 + v5 = 0 + 2 = 2<6;

А1B6 : u1 + v6 = 0 + 0 = 0=0;

А2B1 : u2 + v1 = 0 + 1 = 1= 1;

А2B2 : u2 + v2 = 0 + 4 = 4>3;

А3B1 : u3 + v1 = 0 + 1 = 1< 4;

А3B2 : u3 + v2 = 0 + 4 = 4> 1;

А3B3 : u3 + v3 = 0 + 1 = 1<2;

А3B4 : u4 + v1 = 0 + 1 = 1<2;

А3B5 : u4 + v2 = 0 + 2 = 2<3;

Опорний план не є оптимальним, тому що існують оцінки вільних клітин для яких ui + vi>cij

А2B2 : u2 + v2 = 0 + 4 = 4>3;

А3B2 : u3 + v2 = 0 + 4 = 4> 1;

Тому від нього необхідно перейти до другого плану, змінивши співвідношення заповнених і порожніх клітинок таблиці. Вибираємо максимальну оцінку вільної клітини (А3B2): 1

Ставимо в ній знак «+». Для визначення клітинки, що звільняється, будуємо цикл, починаючи з клітинки А3B2, та позначаємо вершини циклу почергово знаками «–» і «+». Тепер необхідно перемістити продукцію в межах побудованого циклу. Для цього у порожню клітинку А1B4 переносимо менше з чисел хij, які розміщені в клітинках зі знаком «–». Одночасно це саме число хij додаємо до відповідних чисел, що розміщені в клітинках зі знаком «+», та віднімаємо від чисел, що розміщені в клітинках, позначених знаком «–».

З вантажів хij що стоять в мінусових клітинах, вибираємо найменше, , тобто . Додаємо 10 до обсягів вантажів, що стоять в плюсових клітинах і віднімаємо 10 з Хij, що стоять в мінусових клітинах. В результаті отримаємо новий опорний план. Усі інші заповнені клітинки першої таблиці, які не входили до циклу, переписуємо у другу таблицю без змін. Кількість заповнених клітинок у новій таблиці також має відповідати умові невиродженості плану, тобто дорівнювати (n + m – 1).

Отже, другий опорний план транспортної задачі матиме такий вигляд:

Ai	Bj						ui
	b1 = 100	b2 = 120	b3 = 90	b4=70	b5=80	B6=290
а1 = 300	1 100	4 [-] 110	1 90	5	6	0 « 1 2 3 4 5 6 7 8 9 » К-во Просмотров: 350 Бесплатно скачать Контрольная работа: Математичні моделі задач лінійного програмування >>> Скачать <<< Меню Поиск