Контрольная работа: Метод найменших квадратів

Якщо емпірична функція (1) лінійна відносно параметрів , то нормальна система (3) буде системою з лінійних рівнянь відносно шуканих параметрів.

Будуючи емпіричні формули, припускатимемо, що експериментальні дані додатні.

Якщо серед значень і є від’ємні, то завжди можна знайти такі додатні числа і , що і .

Тому розв’язування поставленої задачі завжди можна звести до побудови емпіричної формули для додатних значень .

Побудова лінійної емпіричної формули. Нехай між даними існує лінійна залежність. Шукатимемо емпіричну формулу у вигляді

, (4)

де коефіцієнти і невідомі.

Знайдемо значення і , за яких функція матиме мінімальне значення. Щоб знайти ці значення, прирівняємо до нуля частинні похідні функції

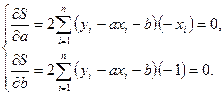
Звідси, врахувавши, що , маємо

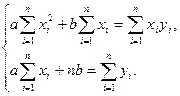(5)

Розв’язавши відносно і останню систему, знайдемо

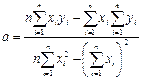, (6)

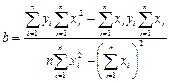. (7)

Зазначимо, що, крім графічного, є ще й аналітичний критерій виявлення лінійної залежності між значеннями і .

Покладемо , , .

Якщо , то залежність між і лінійна, бо точки лежатимуть на одній прямій. Якщо , то між і існує майже лінійна залежність, оскільки точки лежатимуть близько до деякої прямої.

Побудова квадратичної емпіричної залежності. Нехай функціональна залежність між та - квадратична. Шукатимемо емпіричну формулу у вигляді

. (8)

Тоді формулу (2) запишемо наступним чином

Для знаходження коефіцієнтів , , , за яких функція мінімальна, обчислимо частинні похідні , , і прирівняємо їх до нуля. В результаті дістанемо систему рівнянь

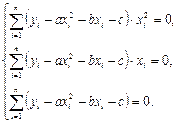
Після рівносильних перетворень маємо систему

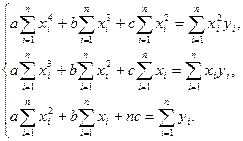(9)

Розв’язок цієї системи і визначає єдину параболу, яка краще від усіх інших парабол (8) подає на розглядуваному проміжку задану таблично функціональну залежність.

Сформулюємо аналітичний критерій для квадратичної залежності. Для цього введемо поділені різниці першого і другого порядку

і , де .

Точки розміщені на параболі (8) тоді і тільки тоді, коли всі поділені різниці другого порядку зберігають сталі значення.