Контрольная работа: Метод простых итераций с попеременно чередующимся шагом

.

Отсюда ,

(4.5)

Из (4.4) и (4.5), двигаясь в обратном порядке, легко получить (4.3). Следовательно, условие (4.3) равносильно совокупности условий (4.4) и (4.5). Из (4.4) и (4.5) получаем следствие:

(4.6)

Докажем сходимость процесса (4.1) при точной правой части. Справедлива следующая теорема.

Теорема: Итерационный процесс (4.1) при условиях , и (4.3) сходится в исходной норме гильбертова пространства.

Доказательство:

.

При условиях , и (4.3) второй интеграл сходится, так как

.

Здесь .

так как сильно стремится к нулю при . Таким образом, . Теорема доказана.

Сходимость при приближенной правой части

Докажем сходимость процесса (4.2) при приближенной правой части уравнения . Справедлива следующая теорема.

Теорема: При условиях , и (4.3) итерационный процесс (4.2) сходится, если выбирать число итераций из условия .

Доказательство: Рассмотрим

.

Оценим , где

Найдём на максимум подынтегральной функции

.

Так как

Если , то

Если , то

при ,

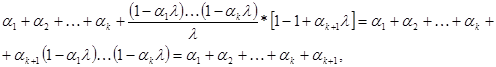
поэтому. Отсюда получим . Поскольку и , то для сходимости метода (4.2) достаточно потребовать, чтобы . Таким образом, достаточно, чтобы . Теорема доказана.

Оценка погрешности