Контрольная работа: Метод простых итераций с попеременно чередующимся шагом

2 случай:

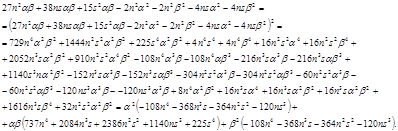
Следовательно:

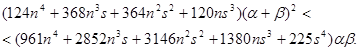
Очевидно, что при условии (4.5) это неравенство справедливо и, следовательно, справедливо (4.11). Итак, при условиях (4.5) и (4.10) справедлива оценка

.

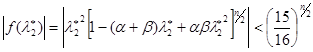На концах отрезка имеем . Таким образом, получим следующие оценки для :

1. в точке ;

2. в точке при условии (4.5) и (4.11) ;

3. в точке .

Найдём условия, при которых , т.е. . Это равносильно условию

. (4.12)

Таким образом, если выбирать и из условия (4.12), то .

Поскольку геометрическая прогрессия убывает быстрее, чем , то для достаточно больших . Поэтому для таких справедлива оценка .

Так как , то при условиях , (4.4), (4.5), (4.10) и (4.12) имеет место следующая оценка погрешности итерационного метода (4.2)

. (4.13)

Нетрудно видеть, что условие (4.12) сильнее условия (4.4). Для нахождения оптимальной по оценки погрешности производную по от правой части выражения (4.13) приравняем к нулю. Тогда оптимальная по оценка погрешности имеет вид

(4.14)

и получается при

. (4.15)

Итак, доказана

Теорема: При условиях , , , (4.10), (4.5), (4.12) оценка погрешности метода (4.2) имеет вид (4.13) при достаточно больших . При этих же условиях оптимальная оценка имеет вид(4.14) и получается при из (4.15).

Таким образом, оптимальная оценка метода (4.2) при неточности в правой части уравнения оказывается такой же, как и оценка для метода простых итераций. Как видно, метод (4.2) не дает преимущества в мажорантных оценках по сравнению с методом простых итераций. Но он дает выигрыш в следующем. В методе простых итераций с постоянным шагом (2) требуется условие , в этом же методе с переменным шагом допускается более широкий диапазон для больших . В методе (4.2) . Следовательно, выбирая и соответствующим образом, можно считать в методе (4.2) примерно втрое меньшим, чем для метода простых итераций с постоянным шагом, и вдвое меньшим, чем для того метода с переменным шагом. Таким образом, используя метод (4.2), для достижения оптимальной точности достаточно сделать итераций соответственно в три раза или два раза меньше. Приведем несколько подходящих значений , удовлетворяющих требуемым условиям:

α	0,8	0,9	1,0	1,1	1,15	1,17	1,3
β	4,4	5,0	5,5	6,1	6,4	6,5	4,1

Наибольшую сумму и, следовательно, наибольший выигрыш в объеме вычислений дают значения и . Поскольку в выделенном случае , то условие (4.6) показывает, что достигнут практически максимальный возможный выигрыш.

Замечание: Оценки сходимости были получены для случая, когда . В случае, когда , во всех оценках следует заменить на .

Замечание: Считаем, что . На самом деле все результаты легко переносятся на случай, когда .

Литература

1. В.Ф. Савчук, О.В. Матысик «Регуляризация операторных уравнений в гильбертовом пространстве», Брест, 2008, 195 стр.