Контрольная работа: Метод простых итераций с попеременно чередующимся шагом
Оценим теперь 
. Покажем, что
, (4.9)
т.е. 
, т.е.
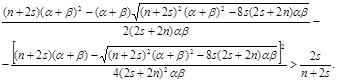
Преобразовав последнее неравенство, получим
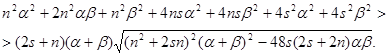
После возведения обеих частей неравенства в квадрат и приведения подобных членов, получим очевидное неравенство
.
В силу равносильности неравенств справедливо неравенство (4.9), так что
.
Таким образом, для 
справедлива оценка
.
Оценим 
в точке
.
Сначала потребуем, чтобы 
, т.е.
.
Усилим неравенство
.
Отсюда 
. При 
, причём, при 
.Пусть 
, тогда при условии
(4.10)
имеем , т.е. 
. В противном случае 
, и оно нас не интересует. Оценим при условии (4.10) функцию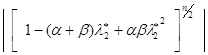 
.
Для этого сначала оценим 
, так как в точке 
функция 
. Найдем, при каких условиях выполняется неравенство
(4.11)
Подставив в (4.11), получим
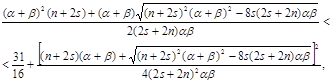
что после упрощения даёт
Возведём обе части неравенства в квадрат, получим
1 случай: