Контрольная работа: Методы формализованного представления систем в исследованиях
Рис. 1 - Классификация методов исследования систем управления
2. МЕТОДЫ ФОРМАЛИЗОВАННОГО ПРЕДСТАВЛЕНИЯ СИСТЕМ В ИССЛЕДОВАНИЯХ
В настоящее время известны различные классификации методов формализованного представления систем. В результате этого методы, иногда возникающие независимо, имеют в основном только терминологические различия. В работе приведена наиболее распространенная классификация, в которой выделяют следующие группы методов формализованного представления: аналитические, статистические, теоретико-множественные, логические, лингвистические, семиотические, графические. Общая направленность классификации следующая: каждая последующая группа методов позволяет формализовать задачу, которая не может быть решена в рамках предыдущей группы методов.
2.1 Аналитические методы
Аналитическими называются методы, в которых ряд свойств многомерной, многосвязной системы отображается в n-мерном пространстве одной единственной точкой, совершающей какое-то движение (рис. 2).
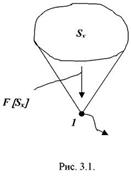
Рисунок 2 – Аналитический метод
Это отображение осуществляется либо с помощью функции f [Sx], либо посредством оператора (функционала) F[Sx]. Можно также две или более систем или их частей отобразить точками, и рассматривать взаимодействие этих точек, каждая из которых совершает какое-то движение, имеет свое поведение. Поведение точек и их взаимодействие описывается аналитическими закономерностями.
Основу терминологического аппарата аналитических представлений составляют понятия классической математики и некоторых новых ее разделов (величина, функция, уравнение, система уравнений, производная, дифференциал, интеграл, функционал и т.д.).
Аналитические методы применяются в тех случаях, когда свойства системы можно отобразить с помощью детерминированных величин или процессов, то есть знания о процессах и событиях в некотором интервале времени позволяют полностью определить поведение их вне этого интервала. Эти методы используются при решении задач движения и устойчивости, оптимального размещения, распределения работ и ресурсов, выбора наилучшего пути, оптимальной стратегии поведения в конфликтных ситуациях и т.п. При практическом применении аналитических представлений для отображения сложных систем следует иметь в виду, что они требуют установления всех детерминированных взаимосвязей между учитываемыми компонентами и целями системы в виде аналитических зависимостей. Для сложных многокомпонентных, многокритериальных систем получить требуемые аналитические зависимости очень трудно. Более того, если даже это и удается, то практически невозможно доказать правомерность применения этих аналитических выражений, то есть адекватность модели рассматриваемой задаче.
2.2 Статистические методы
В тех случаях, когда не удается представить систему на основе детерминированных категорий, можно применить отображение ее с помощью случайных (стохастических) событий, процессов, которые описываются соответствующими вероятностными характеристиками и статистическими закономерностями. ![]() (рис.3).
(рис.3).
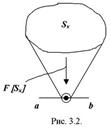
Рисунок 3 – Статистический метод
Размытую точку следует понимать как некоторую совокупность, характеризующую движение системы (ее поведение). При этом границы области заданы с некоторой вероятностью (размыты), и движение точки определяется некоторой случайной функцией. Закрепляя все параметры кроме одного можно получить срез по линии a – b , физический смысл которого – воздействие данного параметра на поведение системы, что можно описать статистическим распределением по этому параметру. Аналогично можно получить двумерную, трехмерную и т.д. картину статистического распределения.
На статистических отображениях базируются математическая статистика, теория статистических испытаний (или статистического имитационного моделирования), частным случаем которой является метод Монте-Карло, теория выдвижения и проверки статистических гипотез, частным случаем которой является байесовский подход к исследованию процессов передачи информации в процессах общения, обучения и других ситуациях, характерных для сложных развивающихся систем.
Статистические отображения позволили расширить области применения ряда дисциплин, возникших на базе аналитических представлений. Так возникли статистическая теория распознавания образов, стохастическое программирование, новые разделы теории игр и др. На базе статистических представлений возникли и развиваются такие прикладные направления, как теория массового обслуживания, теория статистического анализа и др.
Расширение возможностей отображения сложных систем и процессов по сравнению с аналитическими методами можно объяснить тем, что при применении статистических представлений процесс постановки задачи как бы частично заменяется статистическими исследованиями, позволяющими, не выявляя все детерминированные связи между изучаемыми событиями или учитываемыми компонентами сложной системы, на основе выборочного исследования получать статистические закономерности и распространять их с некоторой вероятностью на поведение системы в целом.
Однако не все процессы и явления могут подчиняться статистическим закономерностям, не всегда может быть выбрана представительная выборка, доказана правомерность применения статистических закономерностей, часто для получения статистических закономерностей требуются недопустимо большие затраты времени, что также ограничивает возможности их применения. В этих случаях следует рассматривать возможность применения других методов представления систем.
2.3 Теоретико-множественные представления
Теоретико-множественные представления базируются на понятиях: множество, элементы множества и отношения на множествах. Сложную систему можно отобразить в виде совокупности разнородных множеств и отношений между ними (рис. 4). и названием характеристического свойства (именем, отражающим это свойство) – например, множество A. В основе большинства теоретико-множественных преобразований лежит переход от одного способа задания множества к другому.
В множестве могут быть выделены подмножества. Из двух и более множеств или подмножеств можно, установив отношения между их элементами, сформировать новое множество, состоящее из элементов, качественно отличающихся от элементов исходных множеств.
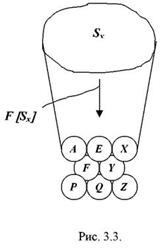
Рисунок 4 - Теоретико-множественные представления
При теоретико-множественных представлениях можно вводить любые отношения. При конкретизации применяемых отношений и правил их использования можно получить одну из алгебр логики, один из языков математической лингвистики. Можно также создать язык моделирования сложных систем, который затем может развиваться как самостоятельное научное направление.
При применении теоретико-множественных представлений для отображения сложных систем и процессов в них наиболее общими формальными характеристиками являются абстрактные знаковые формулы, с помощью которых удобно отображать многоуровневое строение систем. Например, система S может быть отображена в совокупность множеств, описываемую теоретико-множественной формулой:

множество вероятностей p изменения состояний;
![]()
![]() -
-
множество возмущений Z , действующих на систему. Представление системы полной формулой не всегда возможно и целесообразно. Обычно системы описываются сокращенными формулами в зависимости от требований полноты описания.
При отображении системы осуществляется ее декомпозиция – выделение групп (множеств) элементов, обладающих одинаковыми (в рамках определенных ограничений) свойствами. Выделив множества, можно производить соответствующие операции над ними, то есть, ставя их в определенные отношения друг с другом, перейти к композиции системы:
![]()