Контрольная работа: Методы и модели в экономике

-

u₂ =-5

40

10

35

15

0

5

u₃ =-20 v₁ =20 v₂ =15 v₃ =-20

Система для плана имеет вид: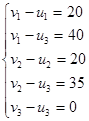

Полагая u₁ =0, находим значения всех потенциалов: (0; -5; -20; 20; 15; -20).

Шаг 2.2. Проверка на оптимальность. Составляем таблицу оценок .

0	-35	-20	u1 =0
-5	0	-15	u2 =-5
∆1 =	0	0	0	u3 =-20
v1 =20	v2 =15	v3 =-20

Так как все оценки ≤0, следовательно, план - оптимальный.

Х _оптим = (0; -5; -20; 20; 15; -20), следовательно, оптимальное значение целевой функции: (руб.).

Ответ: Х _оптим = (0; -5; -20; 20; 15; -20), L(X) = 1625 руб.

Задача №2

2. Решить графически задачу: найти экстремумы функции , если , .

Решить симплекс-методом

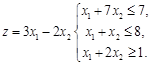
РЕШЕНИЕ

а) Решим задачу графически при

z = 3x₁ – 2x₂ → max

, .

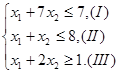
Построим на плоскости прямые ограничений, вычислив координаты точек пересечения этих прямых с осями координат (рис.1).

x 2 16 5

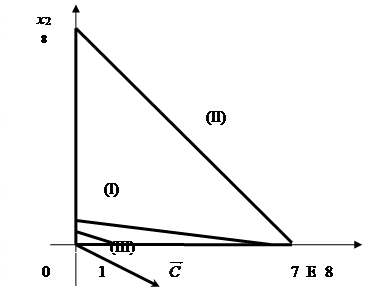
Рис.1. Графическое решение задачи при z = 3x₁ – 2x₂ → max

Строим вектор из точки (0;0) в точку (3; -2). Точка Е (7;0) – это последняя вершина многоугольника допустимых решений, через которую проходит линия уровня, двигаясь по направлению вектора . Поэтому Е – это точка максимума целевой функции. Тогда максимальное значение функции равно:

.

б) Решим задачу графически при